Bisectors of the Angles of the Orthic Triangle

Initializing live version

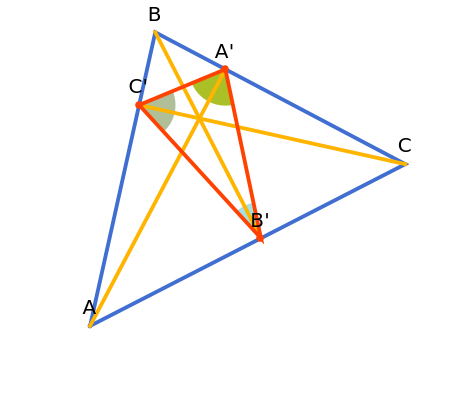
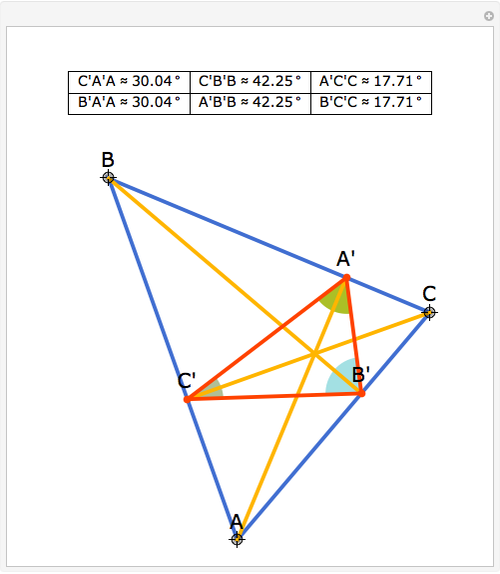
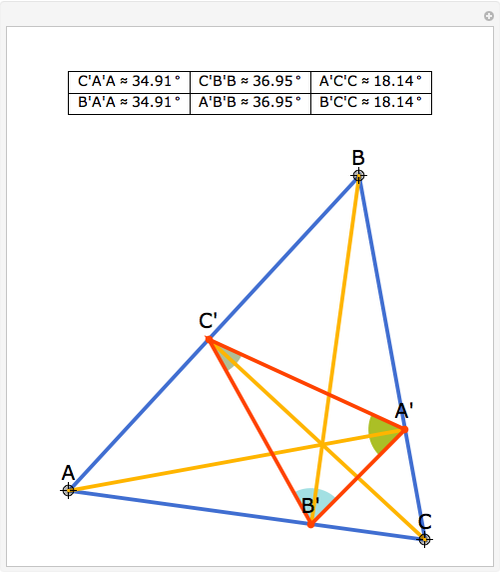
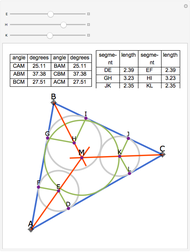
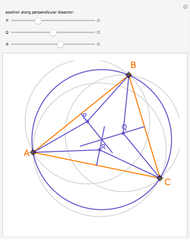
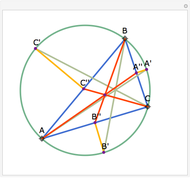
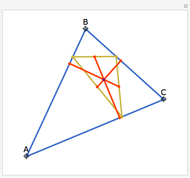
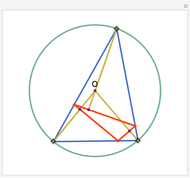
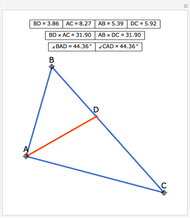
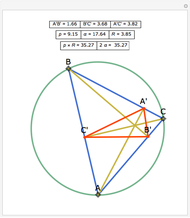
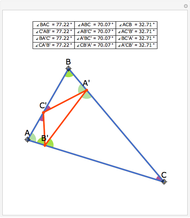
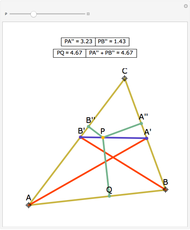
The altitudes of an acute triangle bisect the internal angles of the orthic triangle.

Contributed by: Jay Warendorff (March 2011)
Open content licensed under CC BY-NC-SA

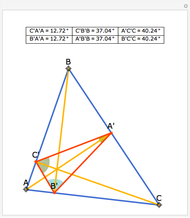
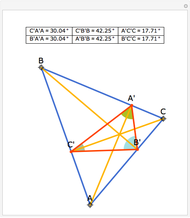
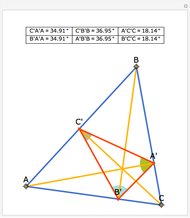
Snapshots

See theorem 192 in N. Altshiller-Court, College Geometry, Mineola, NY: Dover, 2007 p. 98.


Feedback (field required)

Email (field required)	Name

Occupation	Organization

Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback. Send