The Parabola's Evil Twin: Real and Nonreal Roots of a Real Quadratic
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
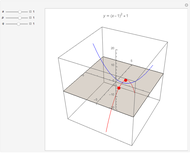
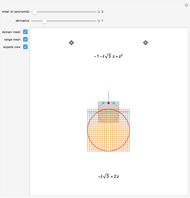
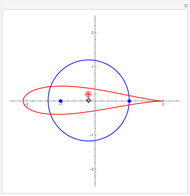
For negative 
, the roots 
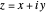of the quadratic equation 
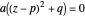are found where the parametric curve 
(the blue parabola) intersects the 
-
plane. However, for positive 
, they are found where 
(the red "evil twin") intersects the 
-
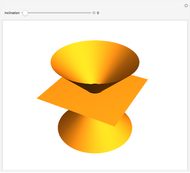
plane. The blue and red parabolas are the intersections of the surface 
with the two vertical planes through its saddle point, parallel to the 
and 
axes, respectively.
Contributed by: Phil Ramsden (December 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The idea for this neat visualization of real and complex-conjugate roots of quadratic equations is due to David Wilson (personal communication).
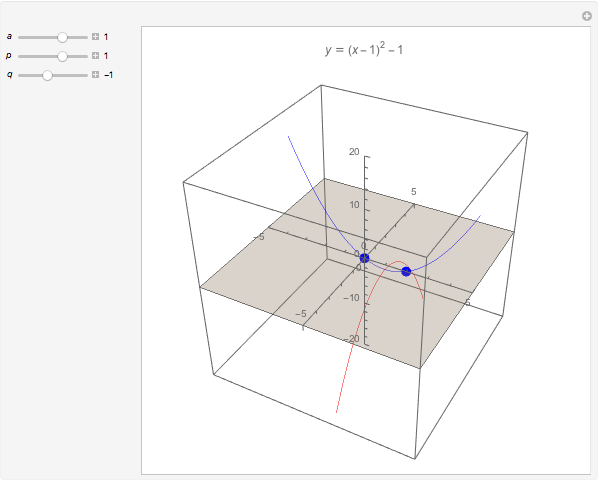
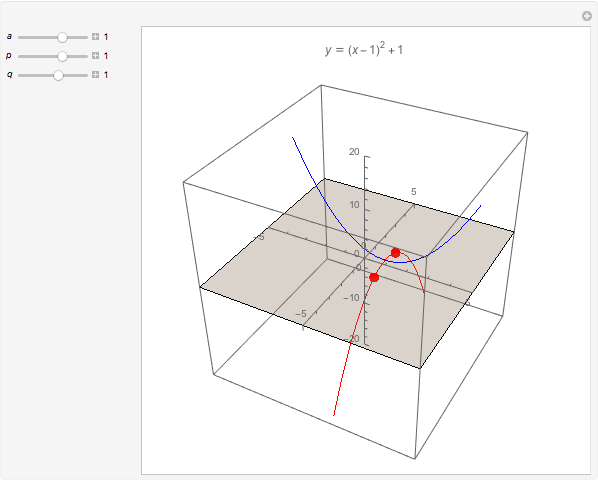
The most important control is the 
slider. The default value of 
is negative; real roots are shown in the 
-
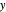plane as blue points. Increase the value of 
and the red "evil twin" takes over; the roots become nonreal and are shown as red points.
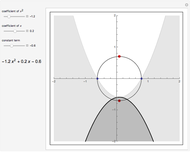
Sliders are also provided for the parameters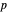 
and 
; it may be instructive to try to predict their effect. What happens when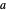 
becomes negative?
Permanent Citation
Locating the Complex Roots of a Quadratic Equation
Jaime Rangel-Mondragon
Complex Roots of a Polynomial and Its Derivative
Michael Schreiber
Quadratic Practice
Michael Ford
Plotting a Parabola
Dean Liming
Constructing Quadratic Curves
Izidor Hafner
Finding a Tangent Line to a Parabola
Jon Mormino
How Does the Vertex Location of a Parabola Change?
Eric Schulz
Two Tangent Lines to a Parabola
Soledad Mª Sáez Martínez and Félix Martínez de la Rosa
Area under a Parabola by Symmetries
Gerry Harnett
Constructing a Parabola from Tangent Circles
Samuel Lesser
-
The Joukowski Mapping: Airfoils from Circles
Phil Ramsden -
Deciding Rain-Affected Cricket Matches: The Duckworth-Lewis Method
Phil Ramsden -
The Great Brachistochrone Race
Phil Ramsden -
Electric Field around a Charged Ring
Phil Ramsden -
The Parabola's Evil Twin: Real and Nonreal Roots of a Real Quadratic
Phil Ramsden -
Fixed Point of a 2x2 Linear System of ODEs
Phil Ramsden -
Conic Sections: The Double Cone
Phil Ramsden -
Discrete Logistic Equation
Phil Ramsden -
Riemann Sums: A Simple Illustration
Phil Ramsden -
Shell Space: The 'Snugness' Condition
Phil Ramsden -
Shell Space: Flare, Verm, and Spire
Phil Ramsden -
Logistic Map: Onset of Chaos
Phil Ramsden -
IFS: Rotation, Translation, and Scaling
Phil Ramsden -
Cumulative Frequency Curves
Phil Ramsden