The Locker Problem

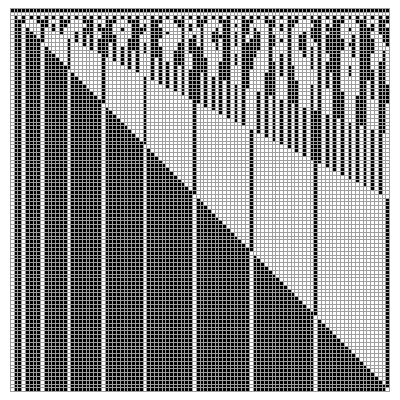
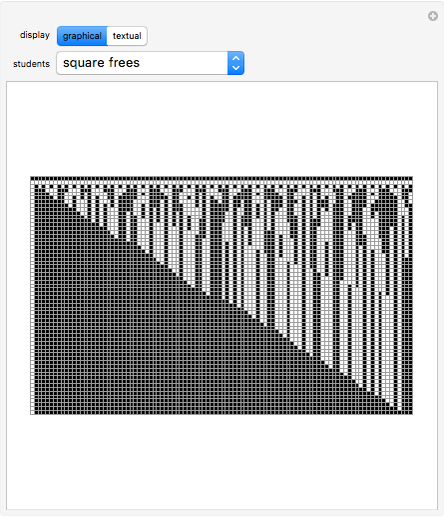
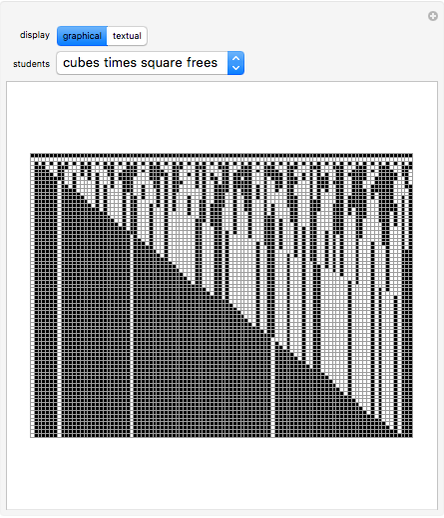
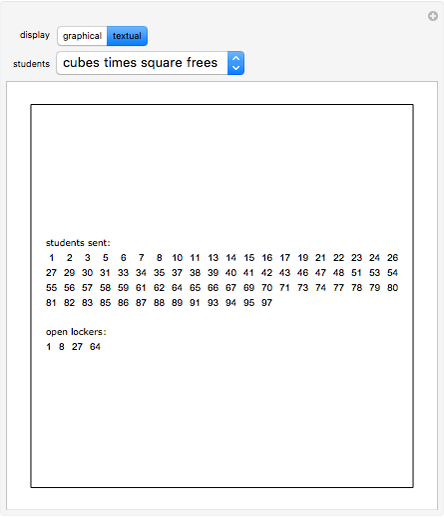
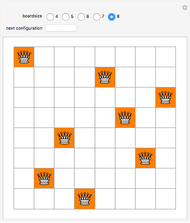
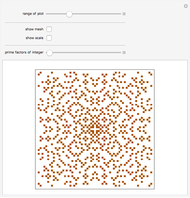
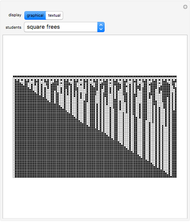
Imagine a hallway with 100 lockers, all closed. 100 students are sent down the hall as follows: student 1 opens all the lockers; student 2 closes every other locker, beginning with the second; student 3 changes the state of every third locker, beginning with the third; and so on. After all the students have marched, which lockers remain open? This Demonstration illustrates the changing locker states as the students march. Black squares represent closed lockers and white squares represent open lockers. The first row in the graphic shows the initial hallway with locker 1 on the left and locker 100 on the right. Each subsequent row shows the hallway after the next student has marched, with the bottom row showing the final locker configuration. The user can select certain subsets of the students to send marching, using the convention that student will change the state of every locker, beginning with the 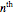. Can you see how the final locker state relates to the set of students sent marching?