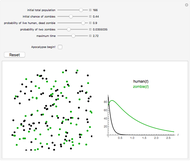
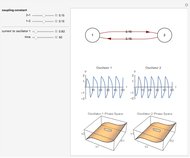
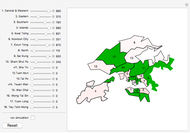
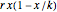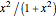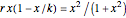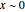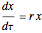Spruce budworm outbreaks are a serious problem in the forests of balsam fir trees in Canada, with these insects feeding on the trees' leaves. A budworm outbreak can cause all the trees in a forest to die within four years.
The proposed model for budworm population dynamics, in dimensionless form, is represented by the equation:
 .
.
In the absence of predators, the population grows logistically as 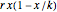 , where
, where  is the growth rate and
is the growth rate and  is the carrying capacity. The death rate term,
is the carrying capacity. The death rate term, 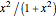 , is due to predation by birds.
, is due to predation by birds.
The steady states are solutions of the equation 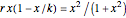 . One can show that
. One can show that  is always an unstable steady state. Indeed, if
is always an unstable steady state. Indeed, if 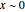 , the governing equation becomes
, the governing equation becomes 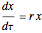 ; thus
; thus  will grow exponentially.
will grow exponentially.
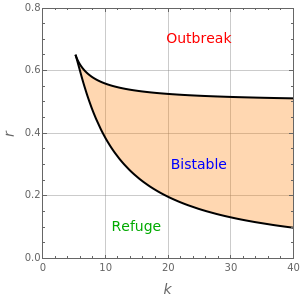
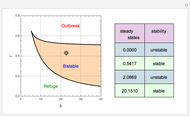
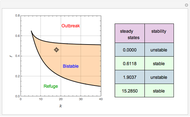
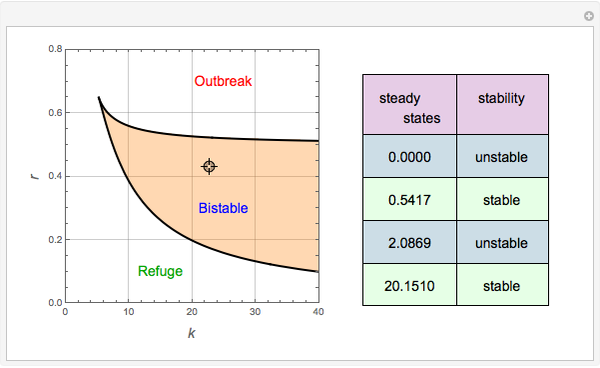
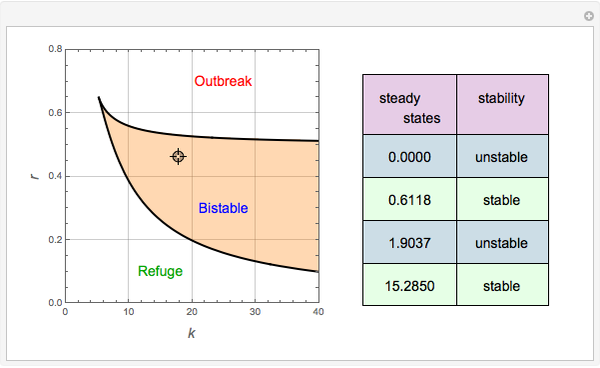
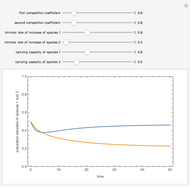
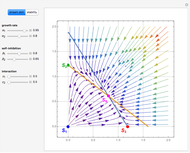
There are up to four steady states for specific values of the parameters  and
and  (
( is in the region indicated by the orange color).
is in the region indicated by the orange color).
When there are only two steady states, since  is unstable, the other steady state is necessarily stable because stability types must alternate. If this steady state corresponds to a large value of
is unstable, the other steady state is necessarily stable because stability types must alternate. If this steady state corresponds to a large value of  , we get an outbreak of budworms resulting in forest destruction. On the other hand, if this second steady state has a small value of
, we get an outbreak of budworms resulting in forest destruction. On the other hand, if this second steady state has a small value of  , we get what is called the refuge level for the budworm population.
, we get what is called the refuge level for the budworm population.
In the event there are four steady states, the refuge and outbreak ones are stable, and one recovers what is commonly referred to as bistability. For this case, the fate of the population depends on the initial condition. Indeed, if the initial condition is above a threshold (i.e. the nontrivial unstable steady-state value), then an outbreak of budworms will occur.
You can drag the locator to select the different values of  ; the Demonstration then computes the corresponding steady states.
; the Demonstration then computes the corresponding steady states.
[less]