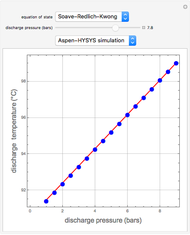
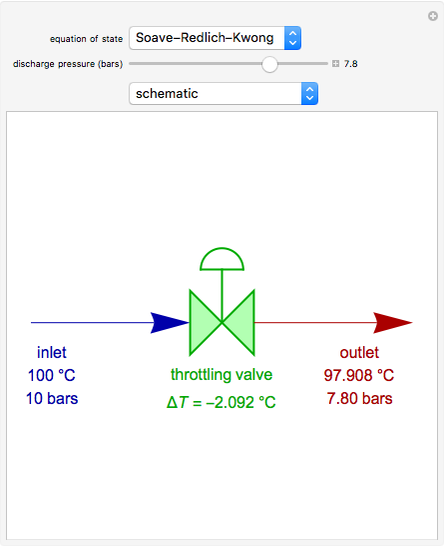
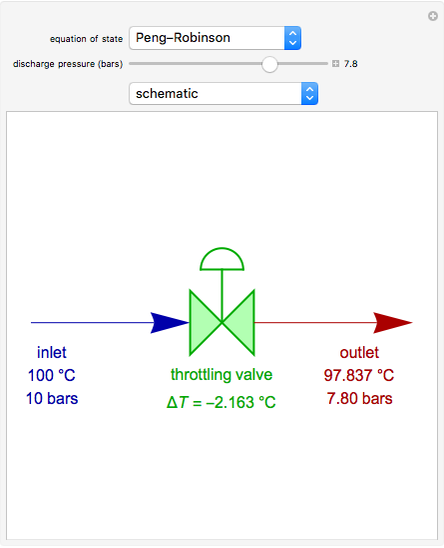
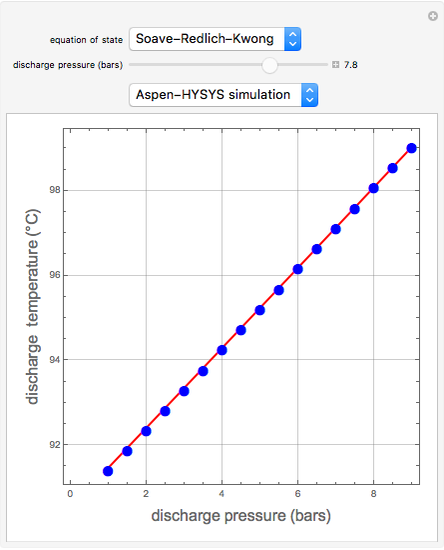
Propylene gas at 100 bar and 373.15 K is throttled to a lower pressure selected by the slider. The process does not produce any shaft work. In addition, there are no appreciable changes in the kinetic or potential energies. Thus, if the process is adiabatic, we get a reduction of pressure at constant enthalpy (or ). This means that for an ideal gas , since the enthalpy of an ideal gas is a function of temperature only. For most real gases, a reduction in pressure at constant enthalpy leads to a reduction in temperature (i.e. ). Indeed, this situation corresponds to a positive Joule–Thompson coefficient, .