Buoyancy of a Balloon
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
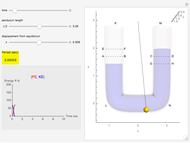
This Demonstration shows the relationship between the buoyant force and the force of gravity acting on an object. A spherical balloon, for which you can vary the radius and the density of the enclosed gas, is attached to a box, which you can vary in mass. For the system to rise, the buoyancy must be greater than the weight.
Contributed by: Zachary Hebebrand and James Drost (June 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Snapshot 1: The buoyancy of the balloon (around 
) is greater than the weight of the box (around 
) due to the increased radius of the balloon, so the system rises. The balloon has risen from its initial point with the increase in the time slider.
Snapshot 2: The buoyancy of the balloon (around 
) is again greater than the weight of the box (around 
), mainly due to the increased density of the gas within the balloon, so the system rises.
Snapshot 3: The buoyancy of the balloon (around 
) is less than the weight of the box (around 
). The entire system stays in the same position due to the weight of the box.
The density of the balloon cannot be less than the density of hydrogen at 1 atmosphere (
). The density within the balloon varies from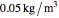 
to 
.
References
[1] L. Taylor. "Practical Buoyancy Control." (May 17, 2014) www-personal.umich.edu/~lpt/practical.htm.
[2] C. Ophardt. "Density Applications with Gases." (May 17, 2014) chemistry.elmhurst.edu/vchembook/imagespdb/123Adensitygas.html.
Special thanks to: The University of Illinois NetMath Program and the Mathematics Department at William Fremd High School.
balloon
box
buoyancy
weight
Archimedes Principle
density
mass
Permanent Citation
Motions of a Simulated Damped Harmonic Oscillator
Teun Zijp
Forces on a Partially Submerged Gate
Rachael L. Baumann
Active Shock Absorbers
Enrique Zeleny
Manometers
Rachael L. Baumann
Analogous Oscillations of a Pendulum and Liquid in a U-Tube
Conrad Benulis
Fracture Element in Rheological Models
Mark D. Normand and Micha Peleg
Falling Body with Zero, Linear, or Quadratic Air Resistance
Anne Tabor-Morris
A Contact Element in Rheological Models
Mark D. Normand and Micha Peleg
Creep and Stress Relaxation for Four-Element Viscoelastic Solids and Liquids
Mark D. Normand and Micha Peleg
Flight of a Glider
Helmut Knaust
