A Contact Element in Rheological Models

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
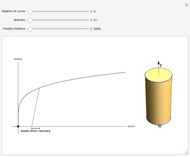
When combined with the traditional elastic and viscous elements, the contact element can describe rheological behaviors characterized by delayed activation. The contact element itself is engaged when the displacement reaches a defined level, which activates the elements with which it is connected. This Demonstration plots the force-displacement curves of simple mechanical analogs composed of a spring, dashpot, and contact element to illustrate the operation of the contact element.
Contributed by: Mark D. Normand and Micha Peleg (October 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Incorporating a contact element in a mechanical analog composed of springs and dashpots can be used to model viscoelastic behavior characterized by delayed activation of the whole or part of the model array. The contact element is defined by: if 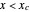 , then
, then 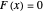 , else
, else 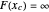 , where
, where  is the displacement in arbitrary length units and
is the displacement in arbitrary length units and 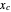 the displacement at which the element is engaged.
the displacement at which the element is engaged.
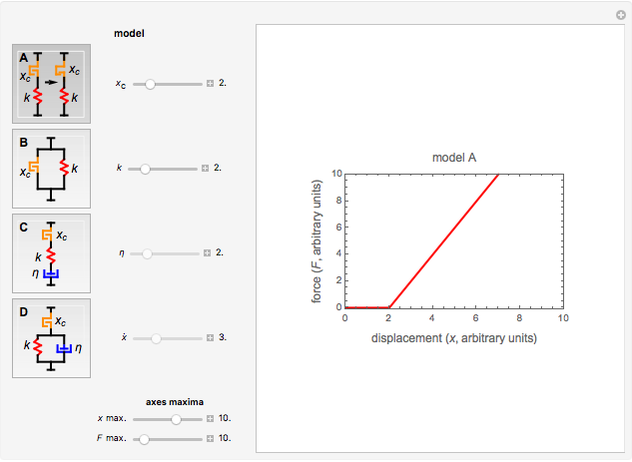
In an in-series combination of the contact element and a spring (model A) the array's definition is: if 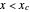 , then
, then 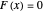 , else
, else 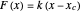 , where
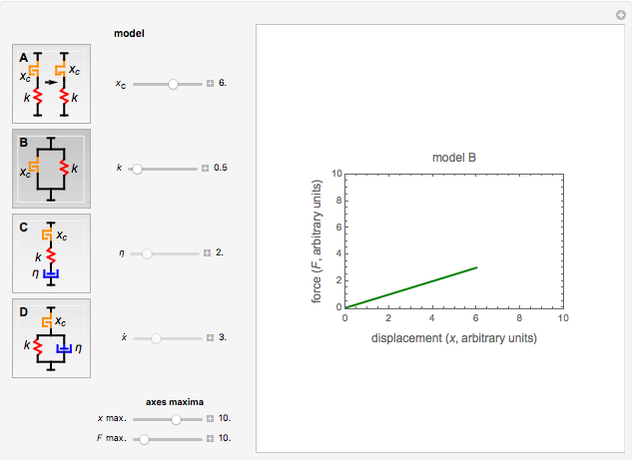
, where  is the spring's constant. In a parallel combination with a spring (model B) the array's definition is: if
is the spring's constant. In a parallel combination with a spring (model B) the array's definition is: if 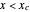 ,
, 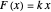 , else
, else  .
.
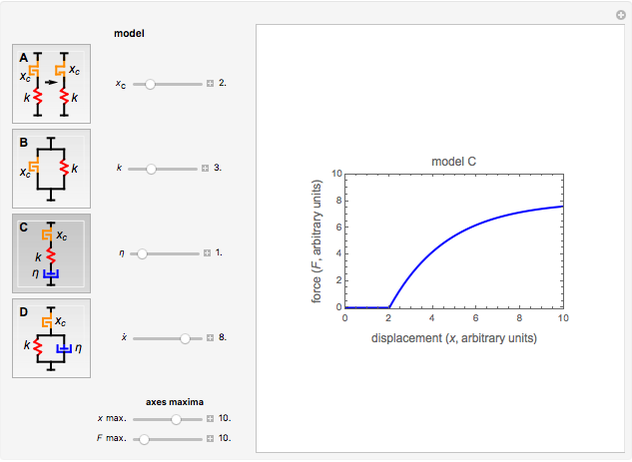
In an in-series combination of the contact element, a spring,  , and a dashpot, η, that is, a Maxwell element (model C), the array's definition is: if
, and a dashpot, η, that is, a Maxwell element (model C), the array's definition is: if 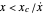 ,
, 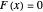 , else
, else 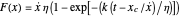 , where
, where  is the displacement rate and
is the displacement rate and 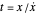 . If the contact element is placed in series with a spring and dashpot themselves in a parallel combination, that is, a Kelvin–Voigt element (model D), the array's definition is: if
. If the contact element is placed in series with a spring and dashpot themselves in a parallel combination, that is, a Kelvin–Voigt element (model D), the array's definition is: if 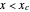 ,
, 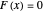 , else
, else 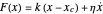 .
.
Notice that in model A, when 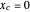 , the resulting plot is of an ordinary spring. In model B, this happens as
, the resulting plot is of an ordinary spring. In model B, this happens as 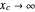 . In model C, setting
. In model C, setting  produces the force-displacement curve of an ordinary Maxwell element and in model D of an ordinary Kelvin–Voigt element.
produces the force-displacement curve of an ordinary Maxwell element and in model D of an ordinary Kelvin–Voigt element.
You can choose the model A, B, C, or D by clicking its setter; then enter the values of 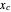 ,
,  , η, and
, η, and 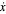 with sliders to plot the corresponding force-displacement curve. You can also enter plot's force and displacement maximum values with sliders.
with sliders to plot the corresponding force-displacement curve. You can also enter plot's force and displacement maximum values with sliders.
Permanent Citation