Constructing a Swung Surface around a B-Spline Curve

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
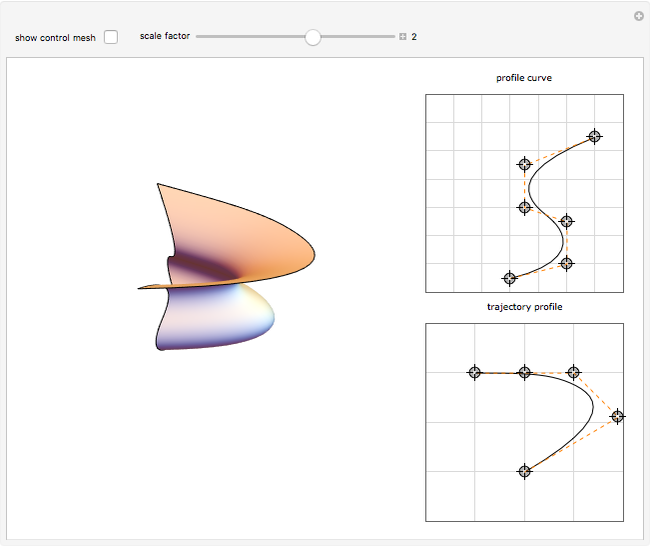
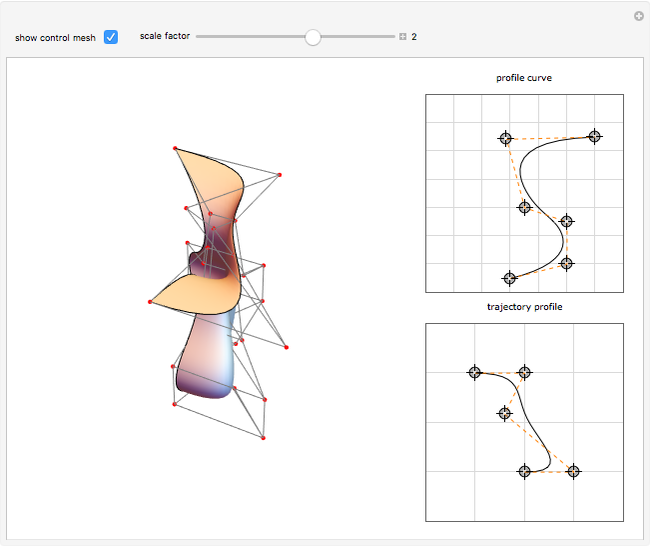
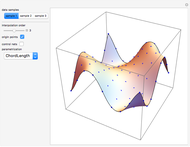
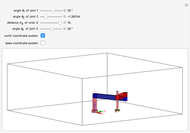
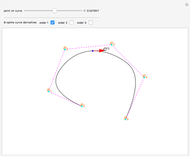
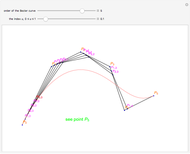
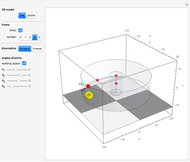
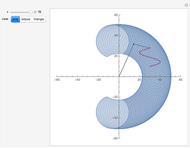
A swung surface is a generalization of a surface of revolution in which the rotation around an axis is governed by a trajectory curve. This Demonstration shows how to generate a swung surface from a B-spline surface. See the Details for a full explanation.
Contributed by: Shutao Tang (November 2015)
(Northwestern Polytechnical University, Xi'an City, China)
Open content licensed under CC BY-NC-SA
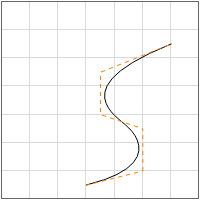
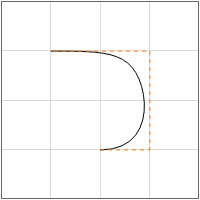
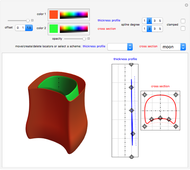
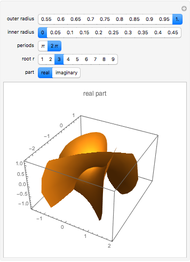
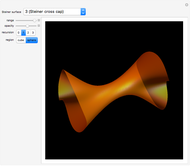
Snapshots
Details
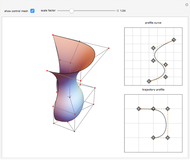
A swung surface is a generalization of a surface of revolution. Let

be a profile curve defined in the 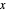 ,
,  plane, and let
plane, and let
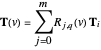
be a trajectory curve defined in the 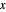 ,
,  plane. Denoting the nonzero coordinate functions of
plane. Denoting the nonzero coordinate functions of 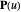 and
and 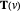 by
by 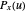 ,
,  ,
, 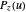 ,
, 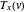 , and
, and 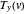 , we define the swung surface by:
, we define the swung surface by:
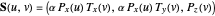 .
.
Geometrically, 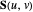 is obtained by swinging
is obtained by swinging 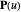 about the
about the  axis and simultaneously scaling it according to
axis and simultaneously scaling it according to 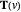 ;
; 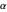 is an arbitrary scaling factor. Fixing
is an arbitrary scaling factor. Fixing  yields curves having the shape of
yields curves having the shape of 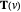 but scaled in the
but scaled in the  and
and  directions.
directions.
Fixing  , the iso-parametric curve
, the iso-parametric curve 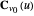 is obtained by rotating
is obtained by rotating 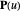 into the plane containing the vector
into the plane containing the vector 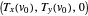 and scaling the
and scaling the 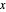 and
and 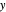 coordinates of the rotated curve by the factor
coordinates of the rotated curve by the factor  . The
. The  coordinate remains unscaled. It follows from the transformation invariance property of NURBS that
coordinate remains unscaled. It follows from the transformation invariance property of NURBS that 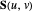 has a NURBS representation given by
has a NURBS representation given by
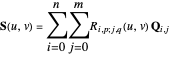
where
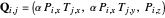
for  ,
,  , and
, and 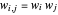 .
.
This Demonstration assumes that the degree of the B-spline curve is 3 and that the initial control points of profile curve and trajectory curve are 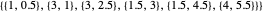 ,
, 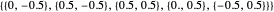 , respectively.
, respectively.
Reference
[1] L. Piegl and W. Tiller, The NURBS Book, 2nd ed., Berlin: Springer–Verlag, 1997 pp. 455–457.
Permanent Citation