Degenerate Critical Points and Catastrophes: Fold Catastrophe

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
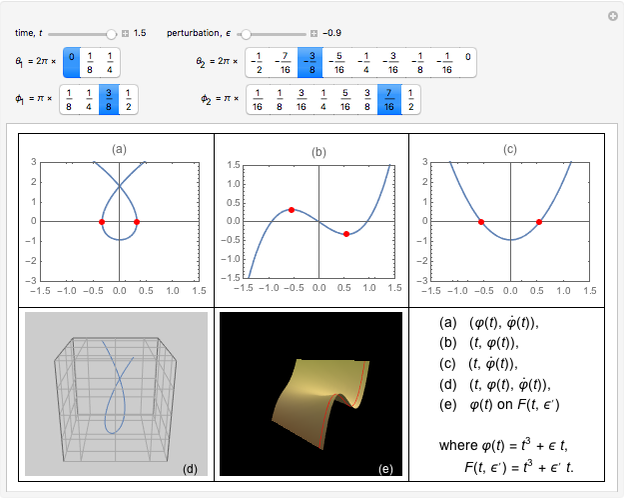
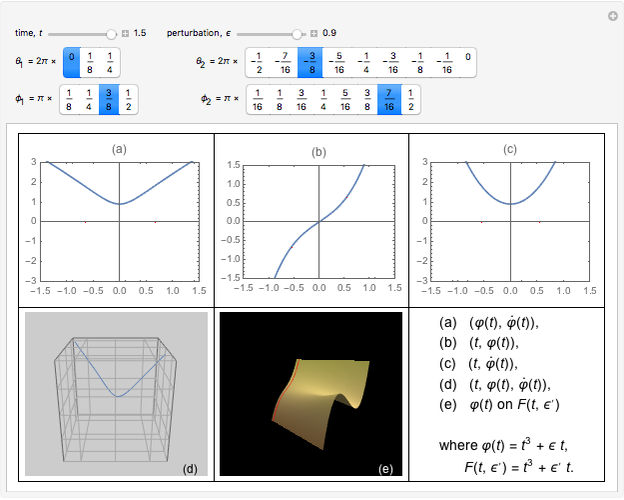
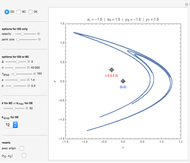
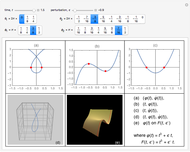
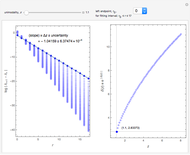
The simple algebraic curve 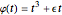 is a good enough example to explain degeneracy and catastrophe in the extended phase space
is a good enough example to explain degeneracy and catastrophe in the extended phase space 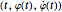 . With the help of this Demonstration, students can easily understand the fold catastrophe.
. With the help of this Demonstration, students can easily understand the fold catastrophe.
Contributed by: Ki-Jung Moon (December 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Bifurcation-catastrophe theorists roughly define a catastrophe as a sudden transition resulting from a continuous parameter change. Here are some basic definitions for understanding the fold catastrophe.
1. A critical point 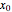 of a differentiable function
of a differentiable function 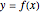 of one variable
of one variable  satisfies
satisfies 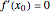 .
.
2. A nondegenerate critical point 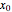 of a differentiable function
of a differentiable function 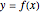 of one variable
of one variable  satisfies
satisfies 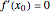 and
and 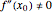 ; if
; if 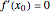 and
and 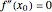 ,
, 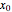 is called a degenerate critical point.
is called a degenerate critical point.
For 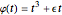 and
and  , there are two nondegenerate critical points; for
, there are two nondegenerate critical points; for  , there is one degenerate critical point; and for
, there is one degenerate critical point; and for 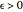 , there are no critical points.
, there are no critical points.
References
[1] V. I. Arnold, Ordinary Differential Equations (R. A. Silverman, ed. and trans.), Cambridge, MA: MIT Press, 1973.
[2] D. V. Anosov et al, eds., Dynamical Systems I: Ordinary Differential Equations and Smooth Dynamical Systems (Encyclopaedia of Mathematical Sciences, Vol. 1), New York: Springer, 1997.
[3] V. I. Arnold, Geometrical Methods in the Theory of Ordinary Differential Equations (J. Szücs, trans.; M. Levi, ed.), New York: Springer-Verlag, 1983.
[4] V. I. Arnold, Mathematical Methods of Classical Mechanics (K. Vogtmann and A. Weinstein, trans.), New York: Springer-Verlag, 1978.
[5] V. I. Arnold, ed., Dynamical Systems V: Bifurcation Theory and Catastrophe Theory (Encyclopaedia of Mathematical Sciences, Vol. 5), New York: Springer, 1994.
[6] V. I. Arnold, Catastrophe Theory, 3rd ed. (G. S. Wassermann, trans.), New York: Springer-Verlag, 1992.
[7] D. P. L. Castrigiano and S. A. Hayes, Catastrophe Theory, Reading, MA: Addison-Wesley, 1993.
[8] R. Thom, Structural Stability and Morphogenesis: An Outline of a General Theory of Models (D. H. Fowler, trans.), Reading MA: Addison-Wesley., 1989.
[9] J. Milnor, Morse Theory, Princeton, NJ: Princeton University Press, 1963.
[10] Y. Matsumoto, An Introduction to Morse Theory (Translations of Mathematical Monographs, Vol. 208) (K. Hudson and M. Saito, trans.), Providence, RI: American Mathematical Society, 2002.
[11] S. H. Strogatz, Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering, Reading, MA: Addison-Wesley, 1994.
[12] S. Wolfram, A New Kind of Science, Champaign, IL: Wolfram Media, 2002.
Permanent Citation