Cellular Automaton Rules on Dendrites

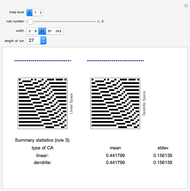
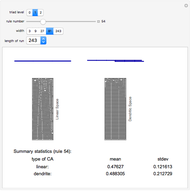
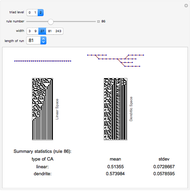
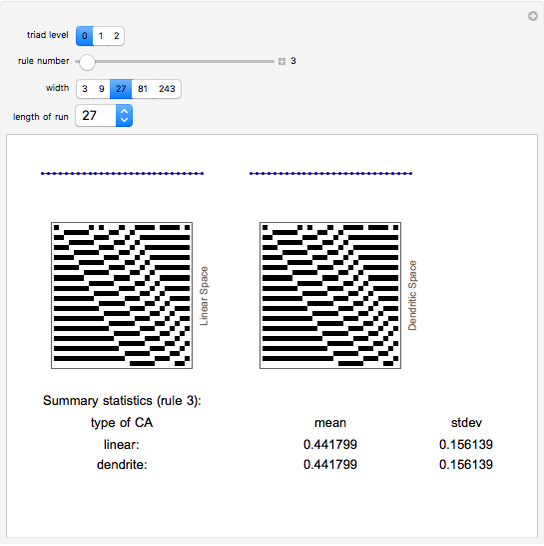
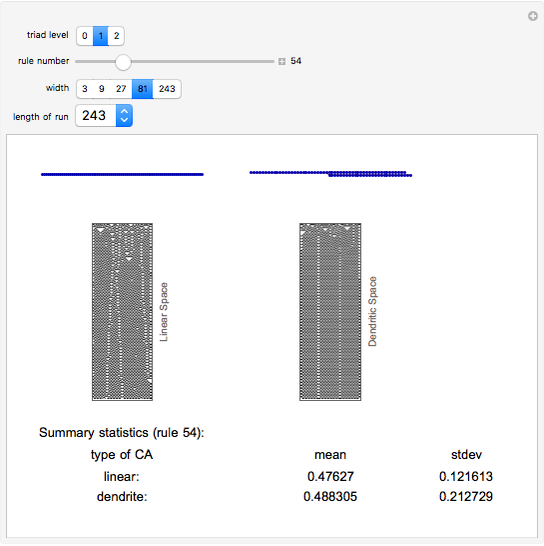
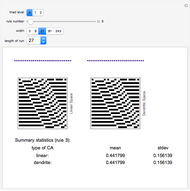
This is an exploration of cellular automaton rules in fractal spaces. It is a simple example using dendrites to generate fractal spaces, where each cell has either one, two, or three neighbors. At the intersections (three neighbors) the standard enumerated (0-255) rules are combined to take a best two out of three to assign that cell. For the most part, the sequences on the dendritic spaces converge to order more quickly than those on the linear spaces. There are some interesting discrepancies in long-term averages and variances of cell values.