The Broken Stick in n Dimensions
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
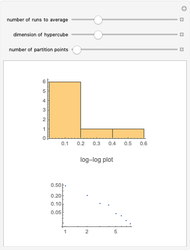
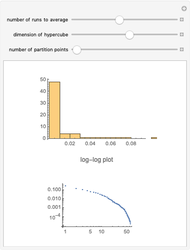
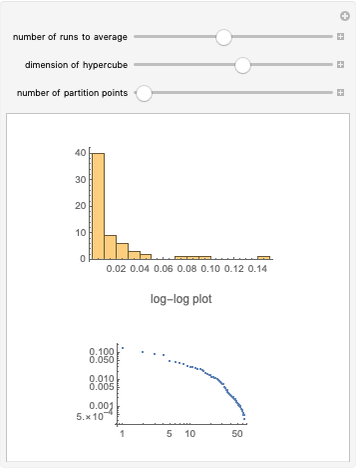
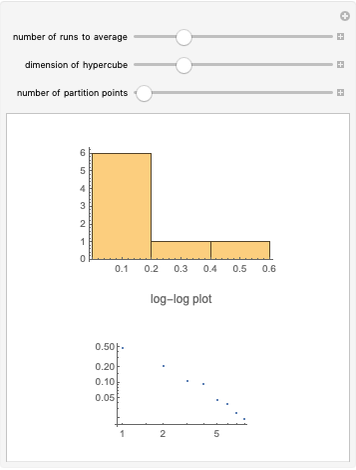
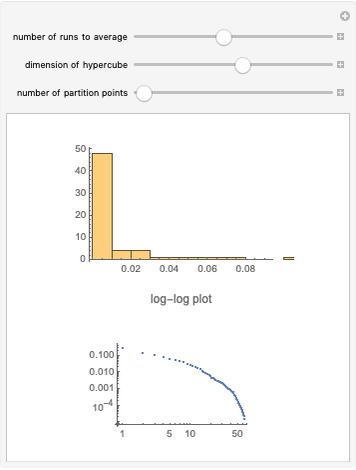
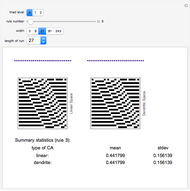
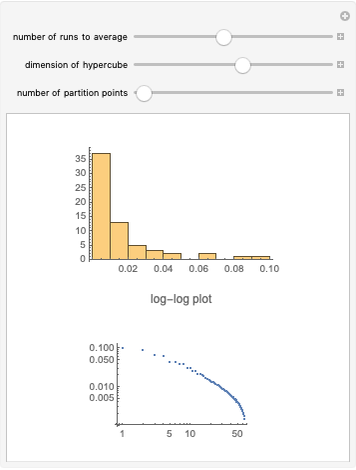
The broken stick problem in  dimensions begins with a unit hypercube and divides it successively by
dimensions begins with a unit hypercube and divides it successively by 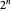 planes perpendicular to the axes into successively smaller rectangular parallelepipeds. At each iteration, only one of the rectangular parallelepipeds is randomly chosen to be divided. Then the resulting distribution of volumes, displayed for any number of iterations, can be seen to show a power-law distribution (graphed in log-log space).
planes perpendicular to the axes into successively smaller rectangular parallelepipeds. At each iteration, only one of the rectangular parallelepipeds is randomly chosen to be divided. Then the resulting distribution of volumes, displayed for any number of iterations, can be seen to show a power-law distribution (graphed in log-log space).
Contributed by: Jim Gerdy (December 2008)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation