Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

House Profits in Negative Edge Games

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

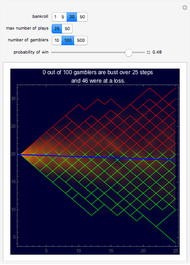
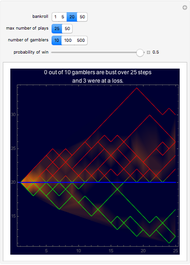
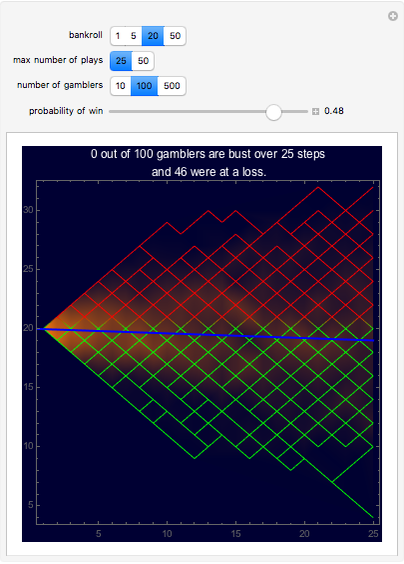
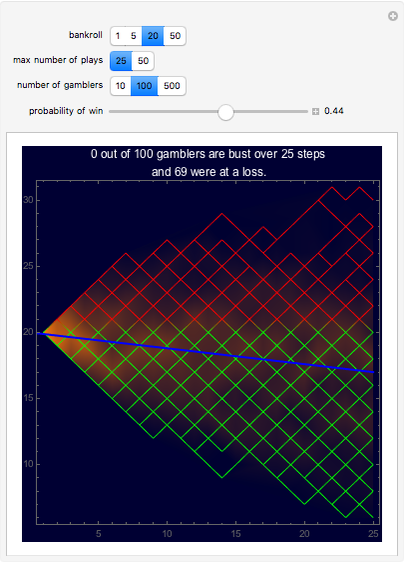
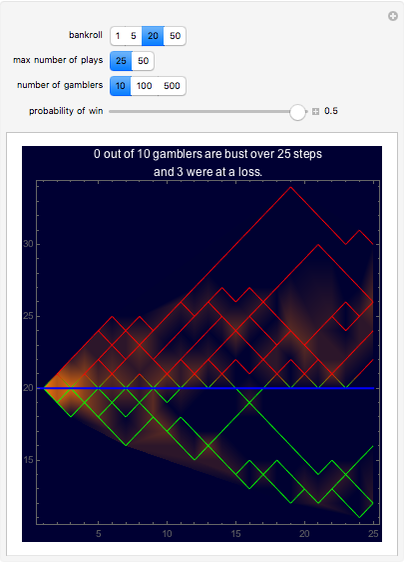
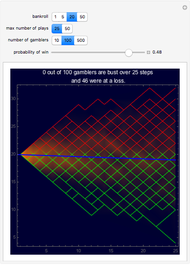
This is a simulation of gambling profits with plots of the profits or losses of individual gamblers along with a density plot of all the gambling together. The gambling consists of successive independent plays to win one unit ($1 for instance) with probability 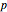and lose one unit with probability , where 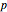ranges from 0.5 down to 0.3, reflecting the negative edge of casino games. The plot also includes a heavy line for the expectation stake of a player after n plays, simply 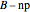, where is the player's initial bankroll. The gambler is busted and play ends when his stake is exhausted.

[more]

Charting shows the perspective of the house where player losses are colored green (as house profits). Also the simulation shows the efficacy of the house odds with in the range of 0.4 to just under 0.5. In this range the gamblers mostly lose money (so the house profits consistently) while most gamblers stay in the game for dozens of plays, with not too many bust. Likewise many common casino games have win probabilities in this range.

[less]

Contributed by: Jim Gerdy (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The selections for length of run are kept relatively short to reflect a casino gambling session. In a casino building players might play for a period of time of a few hours and the house's daily profits depend on the outcomes of these sessions. Since play at most games is a significant fraction of a minute this simulation is intended to reflect the outcome for casual players who play for about an hour. Typical odds must assure the house adequate profits with an ensemble of such players.

The bankroll reflects a typical number of units (dollar value of minimum bet) that a player has in cash entering the casino. 20 is a typical number and a short list in the setter bar, 1, 5, 20, 50, gives a few to choose from. A more detailed study of bankrolling could be done by adding to these choices.

Also as the final thumbnail shows, odds that are too steep on the house's side have a peril too. Much below 0.4 the rate of going bust rises quickly and takes players out of the game.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send