Chaos in the Shift Map

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
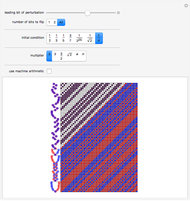
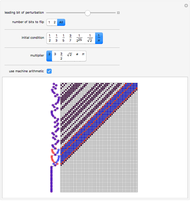
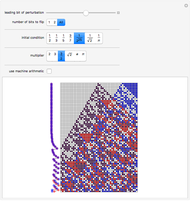
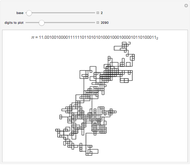
The shift map is a standard example of the sensitive dependence on initial conditions that is at the core of traditional chaos theory. This Demonstration illustrates this basic phenomenon, and shows that there is often more going on in the shift map.
Contributed by: Stephen Wolfram (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
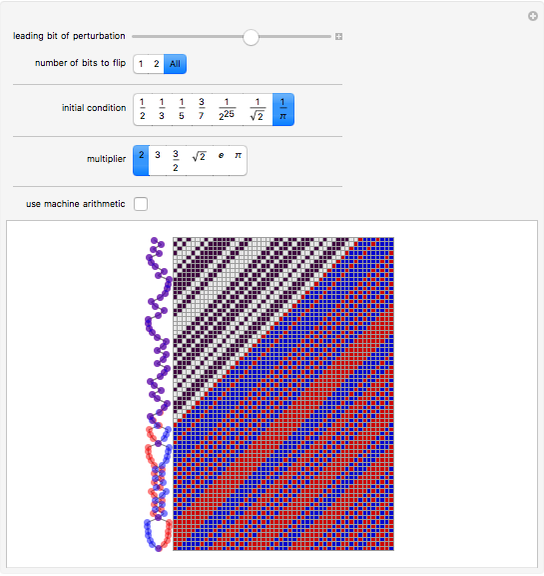
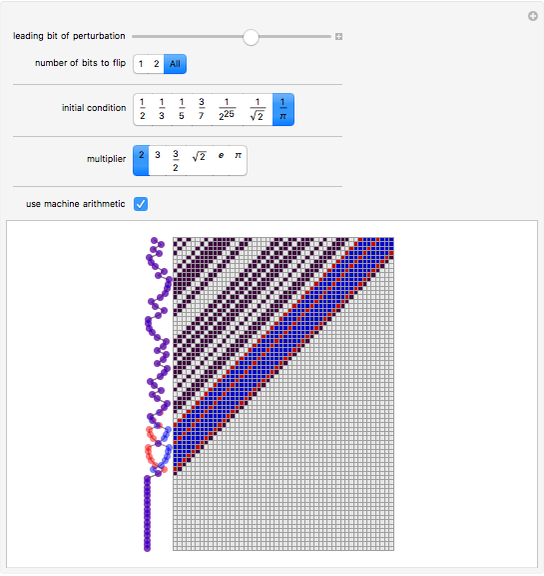
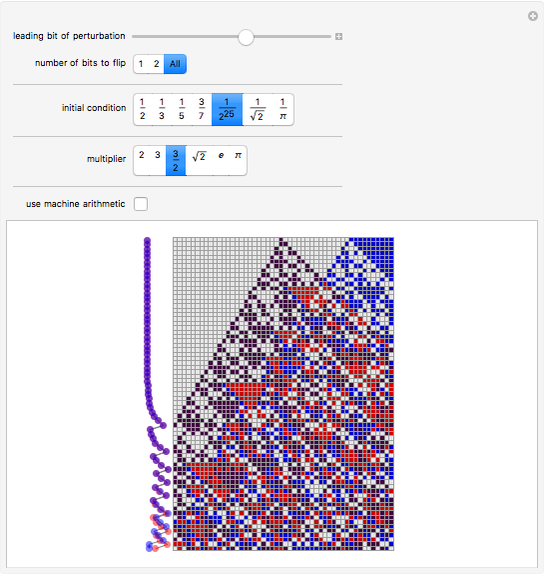
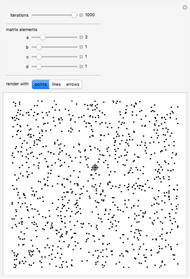
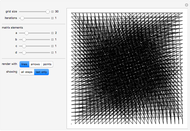
At each step, a number is multiplied by the specified multiplier, but only the fractional part is kept. The main array shows the base-2 digit sequences of successive numbers generated in this way.
One starts with two numbers that differ by a "perturbation" that affects only high-order digits. What the Demonstration shows is that often such a perturbation will grow, as its digits are shifted into more significant positions.
For multiplier 2, all the shift map does is to shift digits to the left. There is apparent randomness in the values shown on the left even in this case, so long as the digit sequence of the initial conditions is somehow seemingly random, say because it comes from a number like 1/π.
If machine arithmetic is used (as in most earlier numerical work), the phenomenon becomes more confused, since after a limited time one "runs out of bits", and starts generating 0s.
With multipliers other than 2, another phenomenon appears: even with very simple initial conditions, apparent randomness is generated, quite independent of "excavating the bits" from the initial conditions. In most practical situations, this is probably a more important source of randomness than the specific one associated with sensitive dependence on initial conditions.
Permanent Citation