Circle Covering by Arcs

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
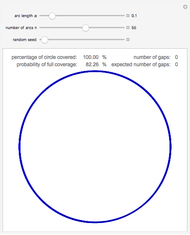
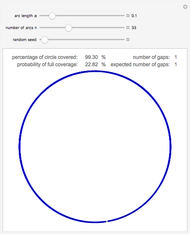
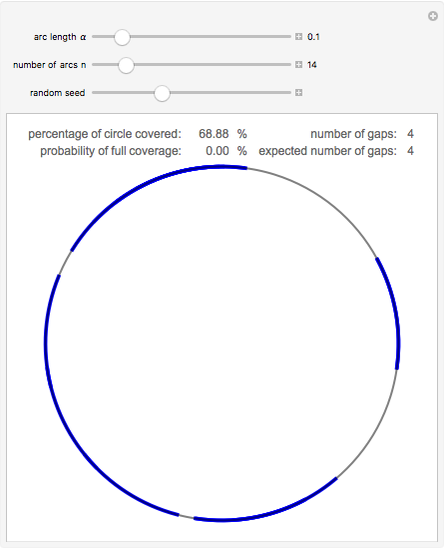
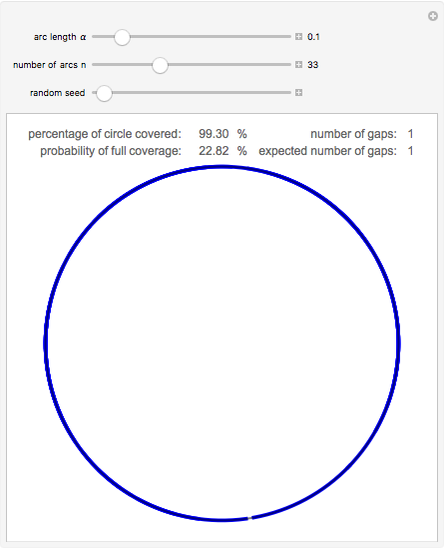
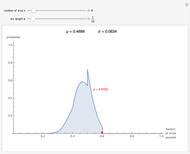
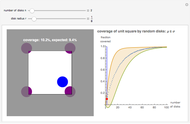
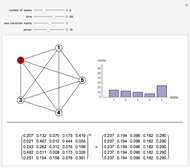
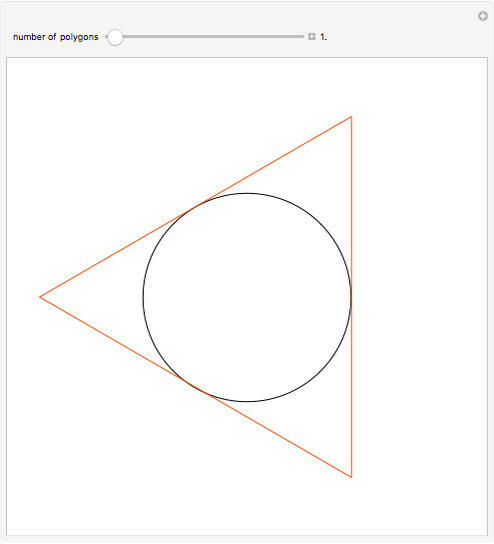
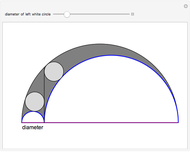
If  points are chosen at random on a circle with unit circumference, and an arc of length α is extended counterclockwise from each point, then the probability that the entire circle is covered is
points are chosen at random on a circle with unit circumference, and an arc of length α is extended counterclockwise from each point, then the probability that the entire circle is covered is 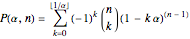 , and the probability that the arcs leave
, and the probability that the arcs leave 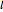 uncovered gaps is
uncovered gaps is 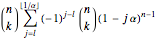 . These results were first proved by L. W. Stevens in 1939. In the image, you can adjust α and
. These results were first proved by L. W. Stevens in 1939. In the image, you can adjust α and  and compare observed circle coverings to the theory. Note that, especially when the arc length is small, there is a reasonable chance that some of the uncovered gaps will be too small to see.
and compare observed circle coverings to the theory. Note that, especially when the arc length is small, there is a reasonable chance that some of the uncovered gaps will be too small to see.
Contributed by: Chris Boucher (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"Circle Covering by Arcs"
http://demonstrations.wolfram.com/CircleCoveringByArcs/
Wolfram Demonstrations Project
Published: March 7 2011