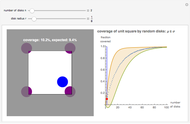
Coverage of a Unit Square by Random Discs

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
If  discs of radius
discs of radius  have centers randomly distributed over the unit square, how much of the square will be covered? What is the underlying probability distribution function?
have centers randomly distributed over the unit square, how much of the square will be covered? What is the underlying probability distribution function?
Contributed by: Aaron Becker (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
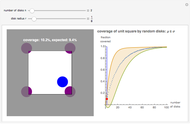
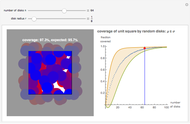
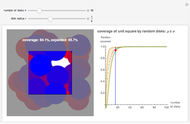
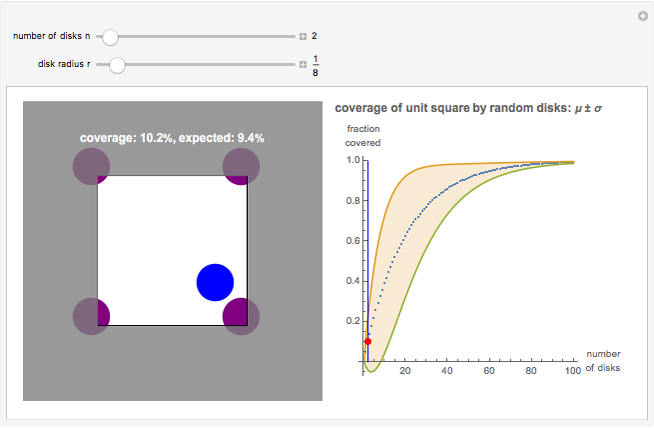
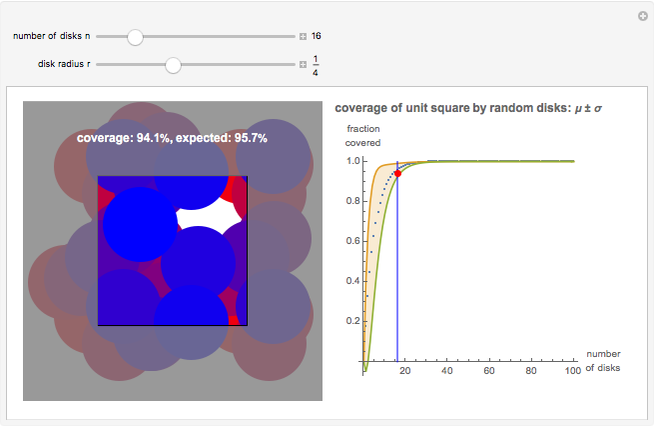
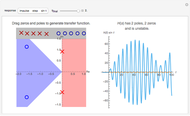
Stochastic coverage processes have medical, military, and natural science applications: respectively, the overlapping disks represent antibodies connected to a virus, the destruction from a bomb drop, and the coverage of a tree canopy. This Demonstration uses the torus convention, where each disk that protrudes from one side of the square is considered to enter the opposite side. This convention simplifies the mathematics, but its effect decreases with  . The left graphic shows a sample run for a given
. The left graphic shows a sample run for a given  and
and  , while the right graphic plots the current coverage overlaid on the mean and variance curves for this
, while the right graphic plots the current coverage overlaid on the mean and variance curves for this  value.
value.
Equations for the mean  and variance
and variance  are given in [1].
are given in [1].
Reference
[1] P. G. Hall, Introduction to the Theory of Coverage Processes, New York: Wiley Series in Probability and Mathematical Statistics, 1988 pp. 24–25.
Permanent Citation