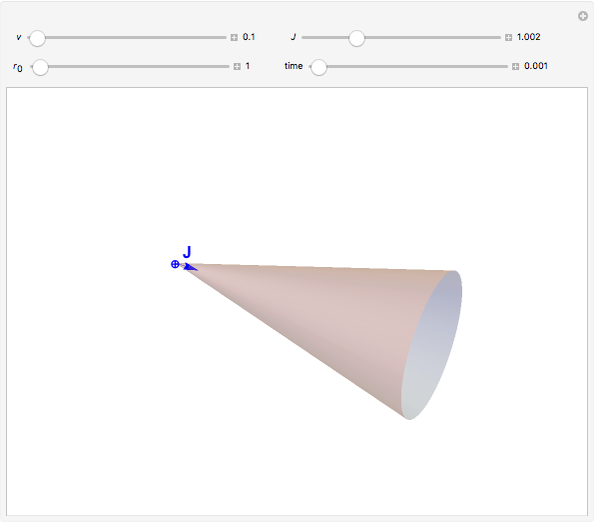
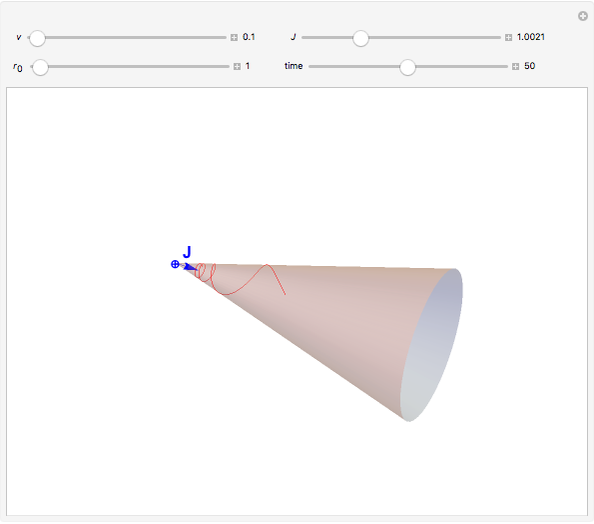
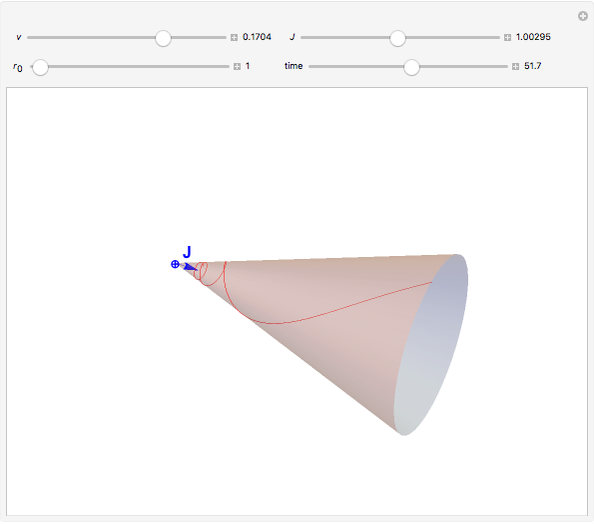
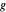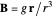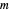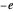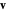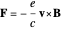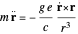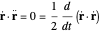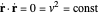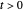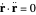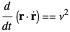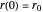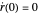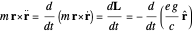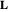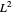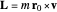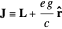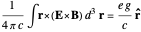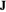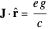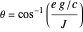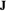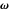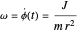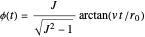Classical Electron in the Field of a Magnetic Monopole

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
To date, there is no conclusive experimental evidence for the existence of magnetic monopoles, the magnetic analog of electric charges. All known magnetic effects arise from magnetic dipoles or from electrical currents. Much of the interest in magnetic monopoles started with a proposal by P. A. M. Dirac in 1931 [1] that if even one magnetic monopole exists in the Universe, a necessary consequence is the quantization of electric charge. Several theories beyond the Standard Model, proposed by 't Hooft, Polyakov, and others, also predict the existence of monopoles. Magnetic monopoles added to Maxwell's equations would create a theory of higher symmetry than the present version of electrodynamics [2].
[more]
Contributed by: S. M. Blinder (August 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The existence of magnetic monopoles would imply the quantization of electric charge. As a major implication in Dirac's paper [1], this is perhaps the most intriguing aspect of magnetic monopoles.
The electromagnetic vector potential 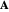 is related to the magnetic induction by
is related to the magnetic induction by 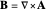 . With
. With 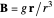 for a magnetic monopole, two possible forms of the vector potential are
for a magnetic monopole, two possible forms of the vector potential are 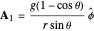 and
and 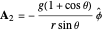 . The first form is singular for
. The first form is singular for 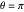 along the negative
along the negative  axis, while the second is singular for
axis, while the second is singular for  along the positive
along the positive  axis. For values of
axis. For values of 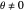 or
or  , either form is valid and they must be related by a gauge condition:
, either form is valid and they must be related by a gauge condition: 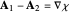 , where
, where 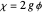 .
.
Gauge invariance in quantum mechanics requires that alternative representations of the wavefunction 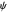 differ by a phase factor
differ by a phase factor  χ/ℏ
χ/ℏ  ), in the present case
), in the present case 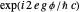 . Comparing the wavefunctions for
. Comparing the wavefunctions for 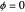 and
and 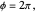 we should find
we should find 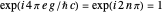 . This implies that
. This implies that 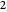
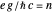 ,
, 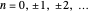 , so that the electric charge
, so that the electric charge  (as well as the magnetic pole strength
(as well as the magnetic pole strength 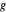 ) must therefore occur as integral multiples of some elementary magnitude.
) must therefore occur as integral multiples of some elementary magnitude.
References
[1] P. A. M. Dirac, "Quantized Singularities in the Electromagnetic Field," in Proceedings of the Royal Society (A133), London: The Royal Society, 1931 pp. 60–72. rspa.royalsocietypublishing.org/content/133/821/60.full.pdf+html.
[2] J. D. Jackson, Classical Electrodynamics, 3rd ed., New York: John Wiley & Sons, 1999 pp. 273–280.
[3] H. Poincaré, Comptes Rendus, 123, 1896 pp. 520–521.
[4] I. R. Lapidus and J. L. Pietenpol, "Classical Interaction of an Electric Charge with a Magnetic Pole," American Journal of Physics, 28(1), 1960 pp. 17–18.
[5] G. Nadeau, "Concerning the Classical Interaction of an Electric Charge with a Magnetic Monopole," American Journal of Physics, 28(6), 1960 p. 566.
Permanent Citation