Complex Pendulum Oscillations at Complex Times

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
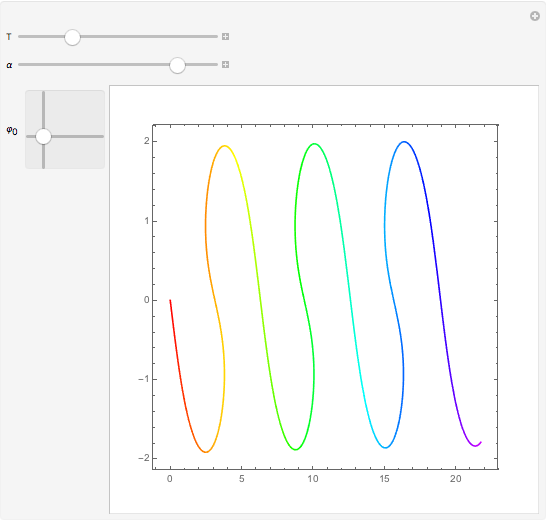
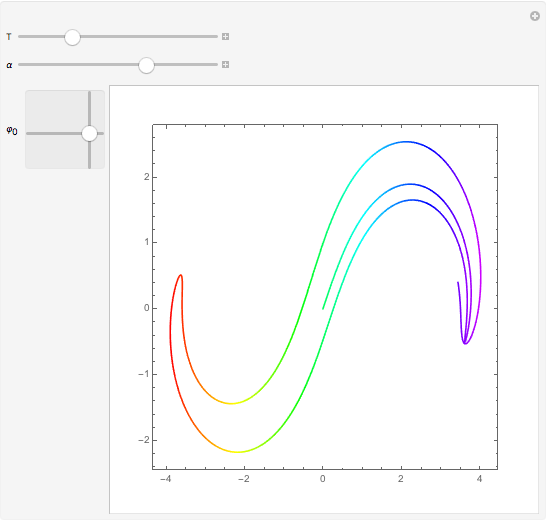
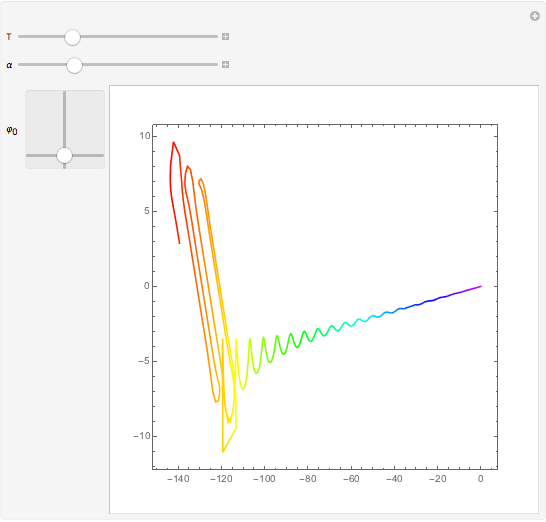
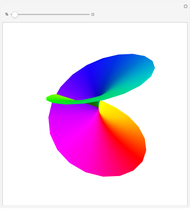
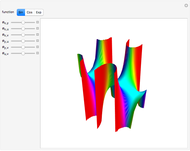
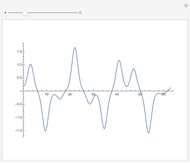
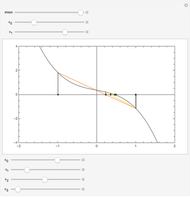
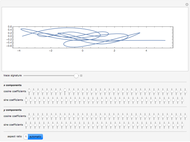
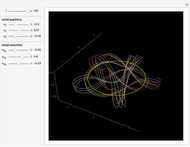
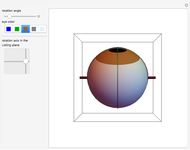
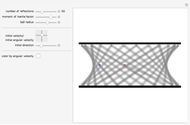
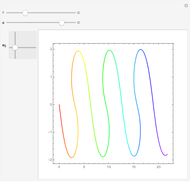
The last few years have seen a rebirth of the importance of complex trajectories. In addition to the classic uses (saddle point approximation of path integrals and complex paths for 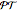 -symmetric Hamiltonians), the transitions on the Riemann surface sheets as a possible (deterministic) explanation of classical chaos are also popular. The pendulum is the perfect example to study complex trajectories. This shows trajectories of a pendulum in the complex plane for complex initial conditions and complex time running along a ray through the origin of the complex time plane.
-symmetric Hamiltonians), the transitions on the Riemann surface sheets as a possible (deterministic) explanation of classical chaos are also popular. The pendulum is the perfect example to study complex trajectories. This shows trajectories of a pendulum in the complex plane for complex initial conditions and complex time running along a ray through the origin of the complex time plane.
Contributed by: Michael Trott (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
 — maximal time
— maximal time
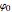 — (complex) initial elongation
— (complex) initial elongation
 — direction
— direction 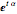 of the ray in the complex time plane
of the ray in the complex time plane
Permanent Citation