Coupled Cellular Automata: Symbiotic Patterns and Synchronization

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
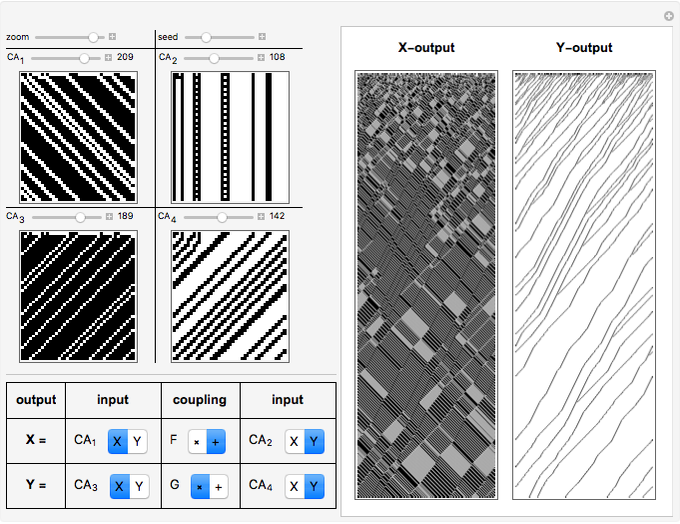
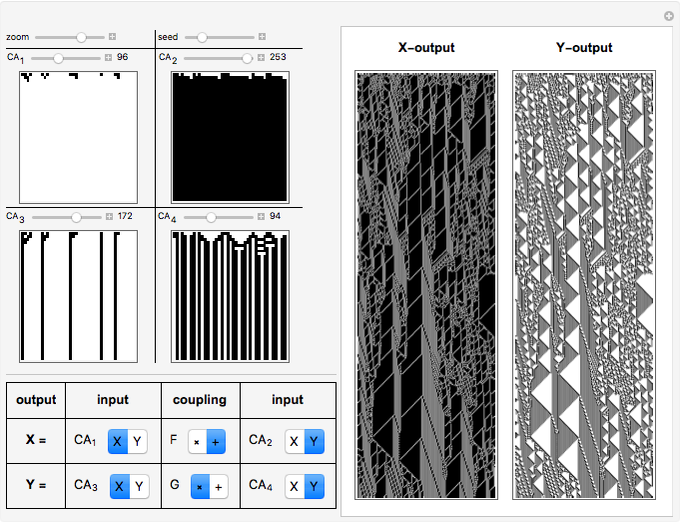
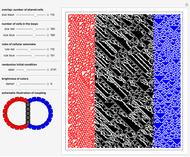
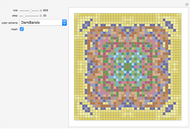
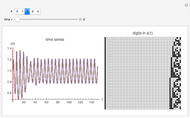
Modeling of cooperative behavior has great relevance to a wide range of scientific fields. Often trivial systems with primitive standalone behavior produce rich dynamics working in collaboration. This Demonstration allows you to couple up to four different one-dimensional elementary cellular automata (1D-eCA) and produce behaviors beyond those of single 1D-eCA. Patterns of these 1D-eCA in the standalone case are shown in four rectangles on the left. They can be compared to the two patterns of coupled evolution on the right (the rectangles labeled 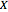 -output and
-output and 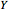 -output). Often, simple evolution of standalone 1D-eCAs results in rich coupled dynamics of
-output). Often, simple evolution of standalone 1D-eCAs results in rich coupled dynamics of 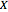 and
and 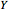 . Such behavior is "symbiotic", since the coupled behavior of
. Such behavior is "symbiotic", since the coupled behavior of 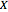 and
and 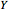 cannot be obtained from standalone 1D-eCA. Another feature of coupled behavior is "synchronization". Namely, the pattern of
cannot be obtained from standalone 1D-eCA. Another feature of coupled behavior is "synchronization". Namely, the pattern of 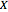 is generally different from the pattern of
is generally different from the pattern of 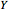 , yet often similar "twin" sub-patterns can be noticed in
, yet often similar "twin" sub-patterns can be noticed in 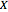 and
and 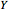 . In all images, the time of evolution goes from top to bottom. The four images on the left are just samples of standard 1D-eCA Wolfram rules. These four images are not used directly to create
. In all images, the time of evolution goes from top to bottom. The four images on the left are just samples of standard 1D-eCA Wolfram rules. These four images are not used directly to create 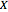 and
and 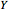 patterns and are given only for comparison with
patterns and are given only for comparison with 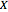 and
and 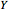 . Browse the snapshots for interesting patterns. See the "Details" section for a more technical discussion of the implemented coupling.
. Browse the snapshots for interesting patterns. See the "Details" section for a more technical discussion of the implemented coupling.
Contributed by: Vitaliy Kaurov (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Controls:
zoom—increase or decrease the size of the initial condition and the length of evolution
seed—randomize the initial condition
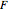 and
and 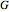 —choose functions (multiplication "×" or addition "+" modulo 2) that couple evolution of
—choose functions (multiplication "×" or addition "+" modulo 2) that couple evolution of 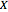 and
and 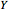 outputs (
outputs (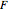 and
and 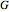 in the formula below)
in the formula below)
Coupling formula description:
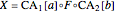 ,
,
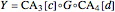 .
.
Each parameter  ,
,  ,
,  ,
,  can be
can be 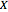 or
or 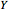 .
. 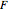 and
and 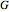 are coupling functions; each can be set to element-by-element multiplication "×" or element-by-element addition "+" modulo 2 of the vectors
are coupling functions; each can be set to element-by-element multiplication "×" or element-by-element addition "+" modulo 2 of the vectors 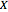 and
and 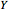 . The result is interpreted again as an IC and repeatedly fed back into the same formulas. The evolution of
. The result is interpreted again as an IC and repeatedly fed back into the same formulas. The evolution of 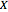 and
and 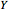 is shown in vertical rectangles on the right, labeled "
is shown in vertical rectangles on the right, labeled "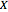 -output" and "
-output" and "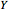 -output".
-output".
Permanent Citation