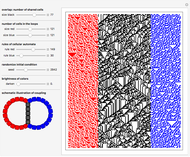
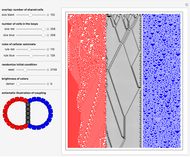
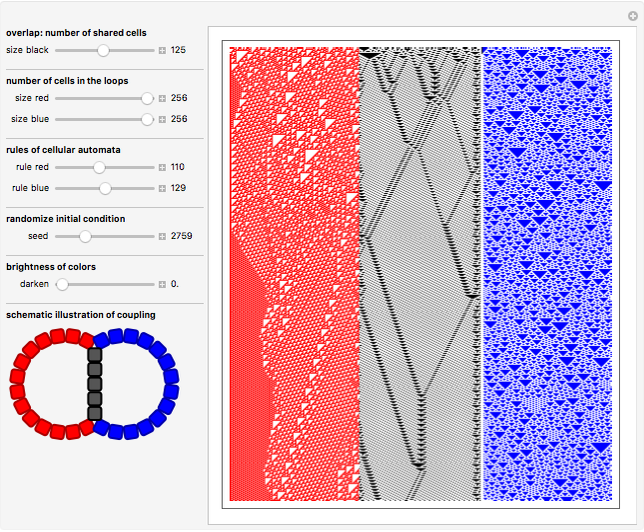
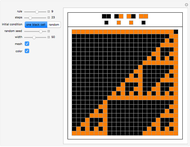
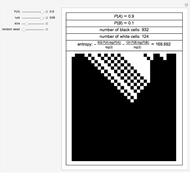
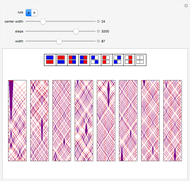
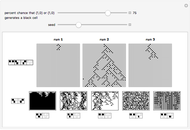
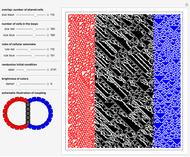
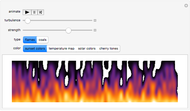
Cellular automata (CA) are often treated as isolated systems with simple cyclic or Dirichlet boundary conditions. Realistic systems, in contrast, interact with the environment through a boundary. Boundaries can be as simple as solid body surfaces, as complex as walls of living cells, or even non-geometric boundaries of social systems. A boundary, having an intricate structure and being a coupling link to the environment, can strongly influence the system dynamics. Here two elementary CA colored red and blue interact via a boundary consisting of black shared cells. The configuration of coupling is schematically shown on the image at the lower-left corner of the graphic. Even the single cell boundary can significantly alter the dynamics of CA, as shown on the fourth row of snapshots. To see clearly whether the dynamics was altered, switch a few times between the given and zero values of the control "overlap" for comparison. If the overlap is made significantly large, it can be considered as a 2-color range-2 CA interacting with two elementary CA. The boundary in this case is the line separating CA of different color. The CA exchange information via the bordering cells. A few examples of cases when the dynamics are significantly altered by the CA coupling are shown on the third row of snapshots. The Demonstration also shows how larger neighborhood CA patterns arise from the multiple action of smaller neighborhood CA. Simply compare the red and blue patterns to the black ones, which should be done with a substantial number of black cells (with the control "overlap" much larger than 5). A few illustrative examples are shown in the first and second rows of snapshots. Browse the bookmarks; for more information, see the Details section.