Iconography for Elementary Cellular Automata Based on Radial Convergence Diagrams
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
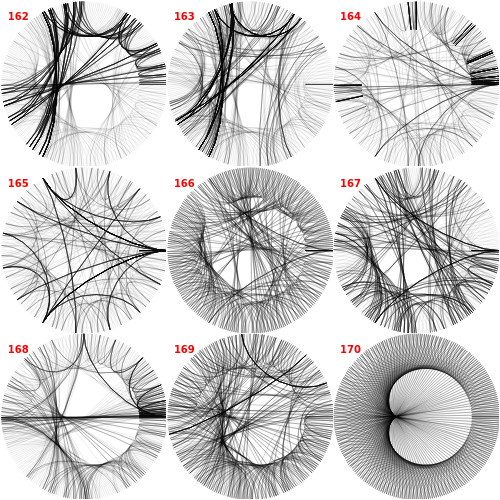
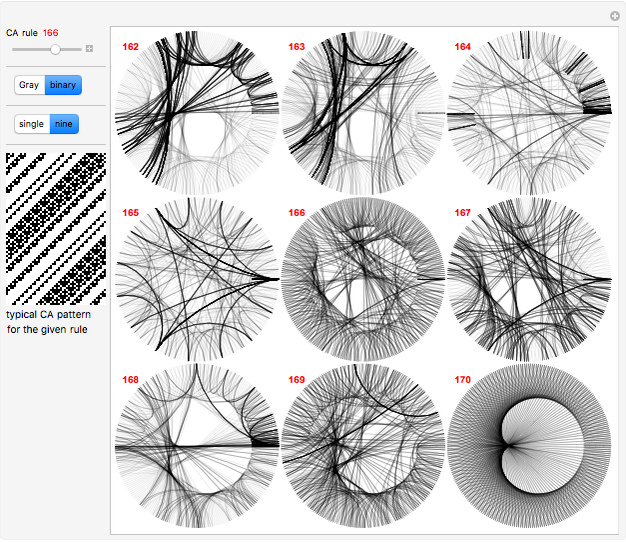
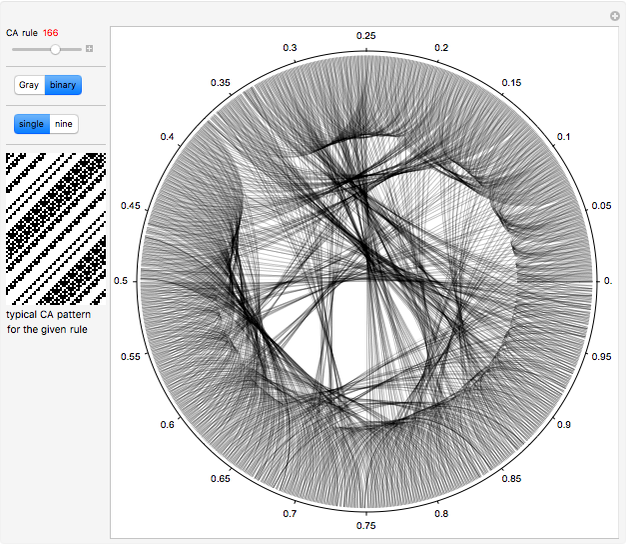
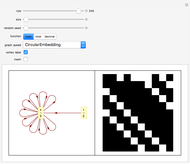
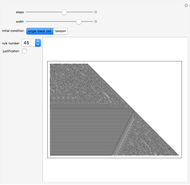
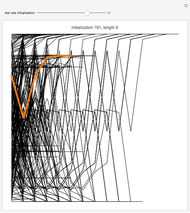
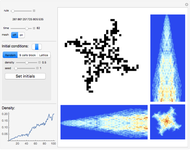
Consider a complete set of initial conditions for a finite elementary cellular automaton (ECA). This set can be indexed by integers using a Gray code or a binary to decimal conversion. During the ECA evolution, the set of such indices is mapped to itself, which can be illustrated with the help of radial convergence diagrams (RCD).
[more]
Contributed by: Vitaliy Kaurov (May 2013)
Open content licensed under CC BY-NC-SA