Two-Dimensional Block Cellular Automata with a 2×2 Neighborhood

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
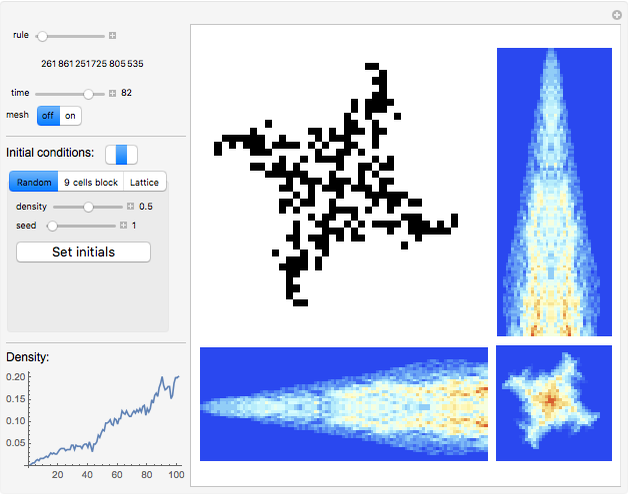
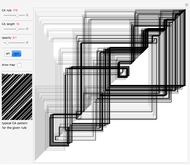
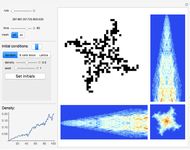
This is a Demonstration for studying two-dimensional block cellular automata (2D BCA) with 2×2 blocks. You can choose any rule from the rule space and trace the evolution of the system through time. Also, you can show the averages over any one of three axes in 3D spacetime and the density evolution plot. Boundary conditions are periodic. There are three types of tunable initial conditions: random initial conditions with a density and a seed parameter, initial conditions with a 3×3 block on the white background, and latticelike initial conditions with black cells with a certain distance between them on the white background. Also there is a collection of interesting rules in the bookmarks.
Contributed by: Teretenkov Alexander (October 2011)
With help provided by: Vitaliy Kaurov
Open content licensed under CC BY-NC-SA
Snapshots
Details
Controls
"rule": The choice of the rule is shown under this control.
"time": The choice of the time step is shown to the right of the control.
"mesh": Select "on" or "off" to show the mesh or not.
"Initial conditions": There are three modes for defining the initial conditions available: "Random", "9 cells block", and "Lattice". The indicator on the left shows which mode is chosen. The mode and its parameters can be chosen in the tab view below.
"Random": This gives random initial conditions with certain density of black cells.
"density": This controls the density of black cells.
"seed": This fixes the SeedRandom parameter allowing one to obtain exactly the same evolution the next time.
"9 cells block": This lets you choose the cells' color in the 3×3 block at the center. Other cells are white.
"Lattice": This gives a regular square lattice of single black cells.
"Size": This lets you choose the period of the lattice.
"Set initials": This button appears in all three cases. It sets the initial conditions in accordance with the chosen mode and its parameters.
"Density": This shows the plot of the black cells density versus time (the step number).
On the right side you can see a certain step of the BCA evolution and averages over certain directions (two space directions and one time direction) of the BCA evolution.
Snapshots/Bookmarks
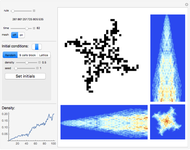
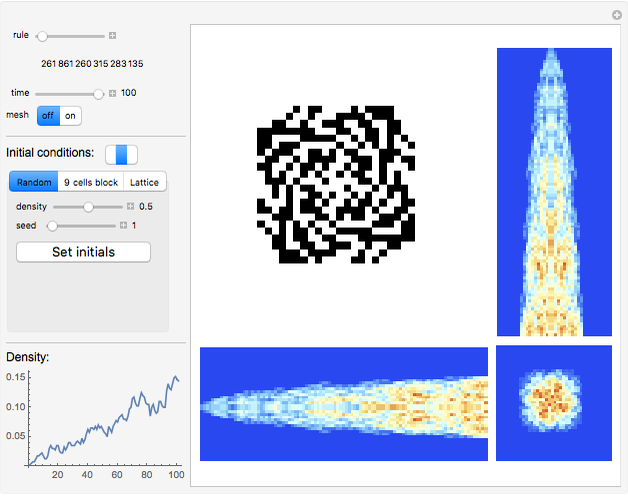
Snapshot 1: twisted star
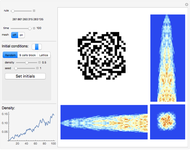
Snapshot 2: flower
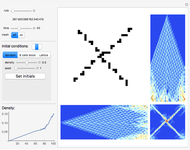
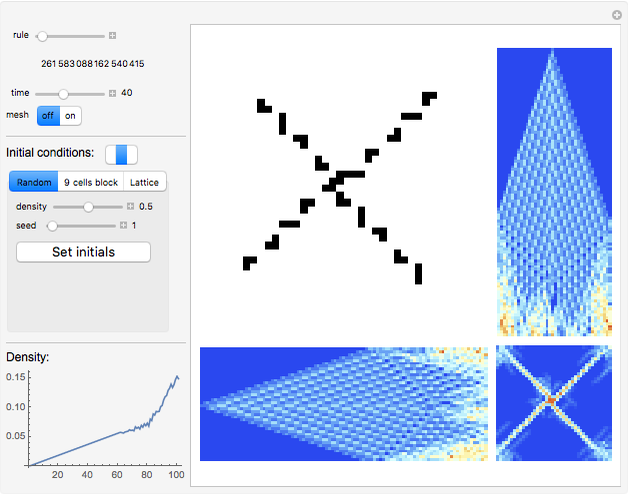
Snapshot 3: particle beams radiator
Bookmark 4: one particle radiator
Bookmark 5: randomness
Bookmark 6: radiating mass
Bookmark 7: regular behavior
Bookmark 8: chessboard generated by mass
Bookmark 9: cluster generation
Bookmark 10: drifting clusters
Bookmark 11: random diamond in frame
Bookmark 12: triangle
Bookmark 13: randomness in frame
Bookmark 14: four particles
Bookmark 15: randomness evolution
Bookmark 16: prime particles
Bookmark 17: ordering
Classification of the Rules
Reversible rules: If for the rule 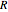 there exists a rule
there exists a rule 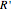 that restores the previous step of the system evolution under
that restores the previous step of the system evolution under 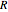 for every system, then
for every system, then 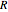 is called reversible.
is called reversible.
Isotropic rules: If after rotating the 2×2 block to which the rule applies, the result after one step in the evolution is also rotated (i.e. operations of the rule application and 2×2 block rotating commute), then the rule is called isotropic.
Overview of the Snapshots
Reversible isotropic rules
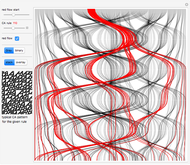
Snapshots 1 and 2 have complicated twisted regular behavior. Snapshots 11 and 13 have random structures surrounded by regular square frames. In snapshot 11 the randomness also shows non-isometric behavior. In Snapshots 3, 4, and 6 you can see particle radiation, which can be one particle radiation as well as radiation of particle beams; the radiating center can be a regular structure as well as a random mass. Snapshot 5 shows random non-isometric behavior of the system in spite of the isometry of the rule itself. Snapshot 12 illustrates the fact that even such simple behavior (a growing triangle) becomes random after reaching the boundary. In snapshot 14 particles fly away from the center and are elastically reflected by the boundary. Snapshot 7 shows interesting regular behavior even after reaching the boundary.
Reversible non-isotropic rules
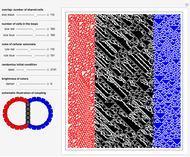
Snapshot 15 shows typical random behavior for a reversible non-isotropic rule with the random boundary evolving just from one cell. In snapshot 8 there is also a typical random mass, but it generates the regular "chessboard" phase.
Irreversible isotropic rules
Snapshots 9 and 10 show the cluster generation. The clusters can be "frozen" (snapshot 9) or drifting (snapshot 10). Also snapshot 7 and snapshot 16 have particles, but these are simply one-cell particles.
Irreversible non-isotropic rule
From any random initial conditions the rule in snapshot 17 evolves the system to the regular gas of moving particles.
Permanent Citation