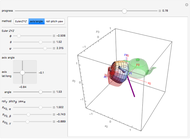
Roll a Sphere without Changing Orientation to a New Location in Two Straight Rolls

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
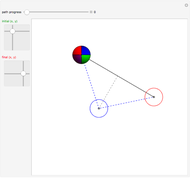
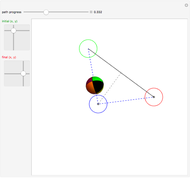
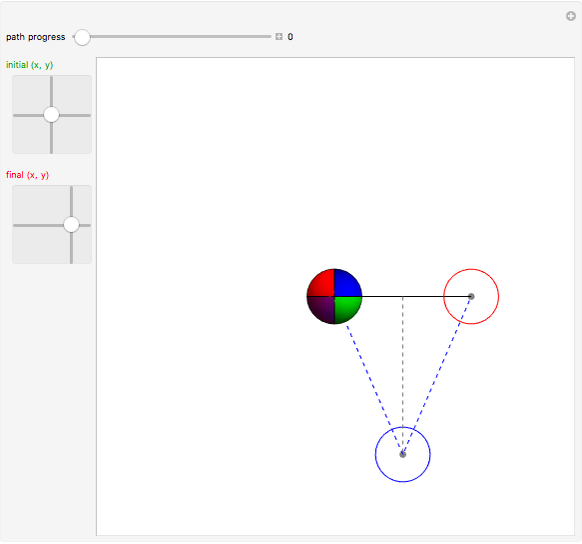
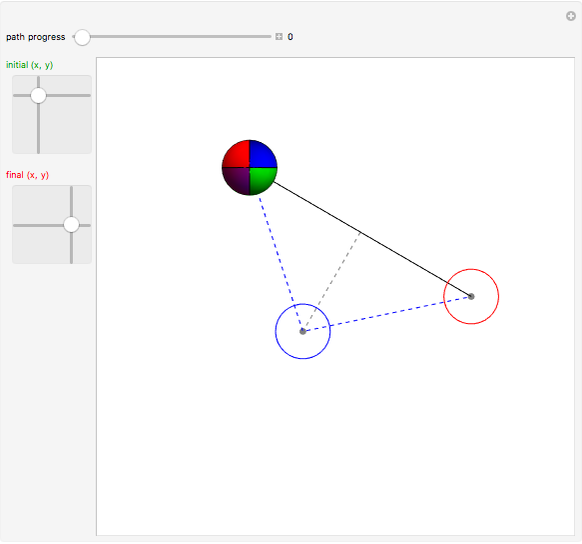
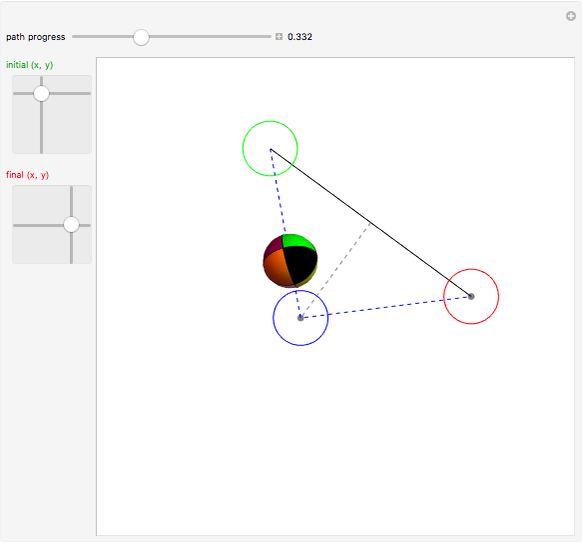
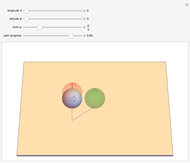
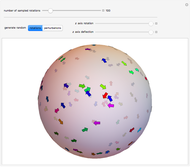
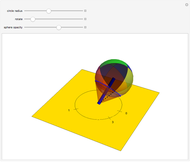
A sphere can be moved to any  location with no net change in orientation by rolling without slipping in two straight-line rolls. Rolling a sphere in a straight line a distance of
location with no net change in orientation by rolling without slipping in two straight-line rolls. Rolling a sphere in a straight line a distance of 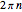 , where
, where  is any integer, returns the sphere to its initial orientation. By combining two such rolls, the sphere can be moved to any
is any integer, returns the sphere to its initial orientation. By combining two such rolls, the sphere can be moved to any  location.
location.
Contributed by: Aaron Becker (August 2012)
After work by: J. M. Hammersley
Open content licensed under CC BY-NC-SA
Snapshots
Details
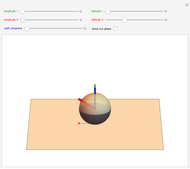
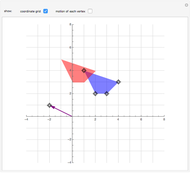
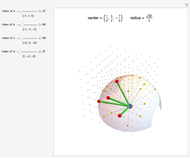
J. M. Hammersley proved that three straight-line rolls in the horizontal plane are sufficient to move a sphere to any desired position and orientation, but that three rolls can lead to arbitrarily long paths. In contrast, the total path length needed to move the sphere from a start position to a desired position at a distance  away without changing orientation is
away without changing orientation is  , where
, where  is the ceiling function. The procedure is to first roll the sphere to a desired orientation with two straight-line rolls, and then move the sphere to the desired position with two straight-line moves.
is the ceiling function. The procedure is to first roll the sphere to a desired orientation with two straight-line rolls, and then move the sphere to the desired position with two straight-line moves.
By applying the Demonstration Re-Orient a Sphere with Two Straight Rolls, followed by this Demonstration, a ball can be rolled to any orientation and position in four rolls.
Reference
[1] J. M. Hammersley, "7. Oxford Commemoration Ball," in Probability, Statistics and Analysis: London Mathematical Society Lecture Note Series, No. 79 (J. F. C. Kingman and G. E. H. Reuter, eds.), Cambridge, UK: Cambridge University Press, 1983.
Permanent Citation