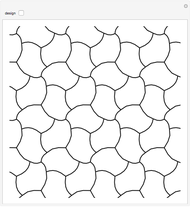
Design a Tile for the p3 Wallpaper Group

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
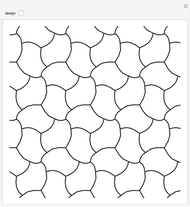
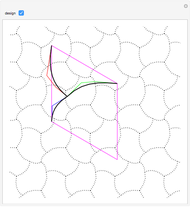
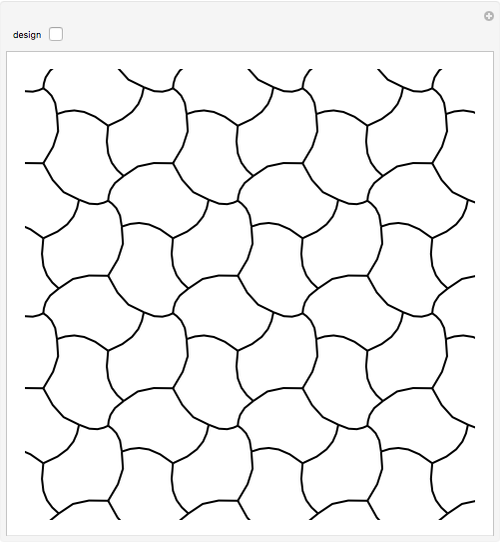
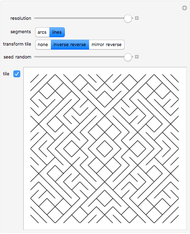
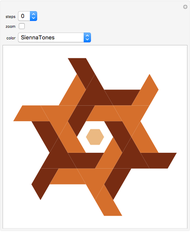
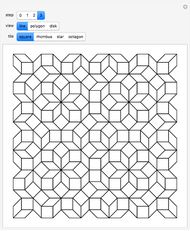
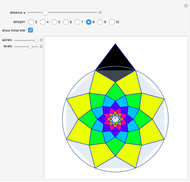
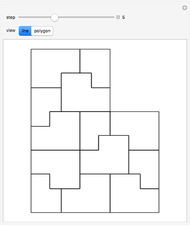
A wallpaper group (or plane symmetry group) describes the symmetries of a two-dimensional repeating pattern. The p3 group can be thought of as a hexagonal lattice, where each hexagon is comprised of three copies of a rhombus rotated around the hexagon's center. This Demonstration lets you change the three spline curves connecting three corners of the rhombus, which gives an interesting tessellation of the plane using a single tile.
Contributed by: Roger Glendenning (March 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"Design a Tile for the p3 Wallpaper Group"
http://demonstrations.wolfram.com/DesignATileForTheP3WallpaperGroup/
Wolfram Demonstrations Project
Published: March 11 2013