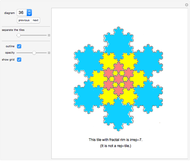
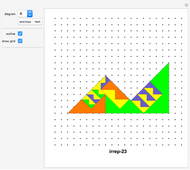
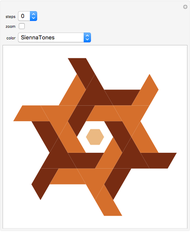
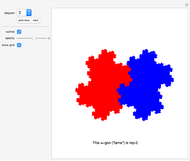
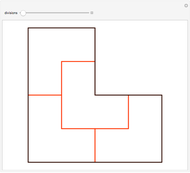
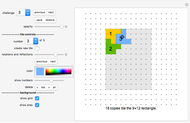
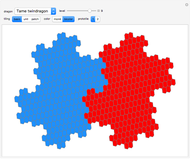
A shape that can tile itself with smaller equally sized tiles is called a rep-tile. If the tiling uses
copies, the shape is said to be rep-
.
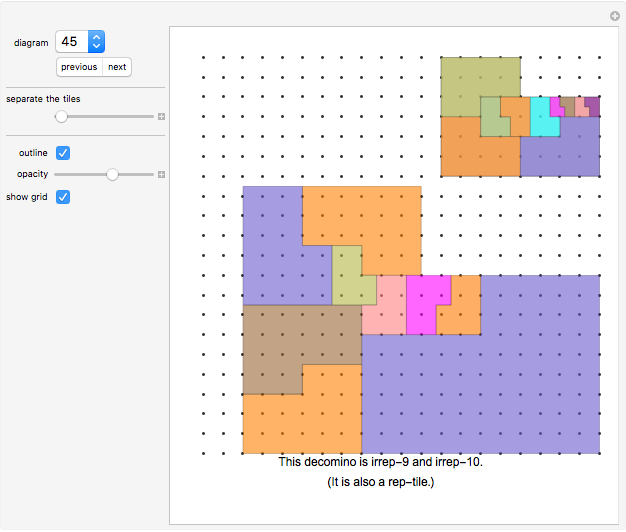
A shape that tiles itself using different sizes is called an irregular rep-tile or irreptile. If the tiling uses
copies, the shape is said to be irrep-
. If all tiles have different sizes the tiling is called perfect.
A shape that only allows irregular self-tilings is called a puritile.
The regular order of a shape is the smallest possible number of tiles in a regular self-tiling.
The irregular order of a shape is the smallest possible number of tiles in an irregular self-tiling (using more than one size of tiles).
The author conjectures that there is no shape where these two orders are the same.
The terms "irreptile" and "puritile" were introduced by the author in 1987 in his book
A Puzzling Journey to the Reptiles and Related Animals, privately published. Since then several mathematicians have expanded on the subject in various ways. To name a few: Michael Reid, Rodolfo Kurchan, Christian Richter.
The material of this Demonstration was mainly taken from the author's book.
Tilings 32, 40, 41, 42, 50, 52, 53, 59 and 60 are by Michael Reid; tiling 51 is by Rodolfo Kurchan.
Of course, this Demonstration can only give a short introduction to irreptiles. Many questions can be asked (and many are answered in the author's book), but several problem areas are still unsolved.
You might want to try to solve some of the many challenges given in diagrams 68 and 69, which this Demonstration can only mention on the side.
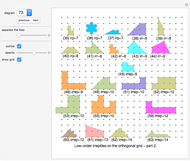
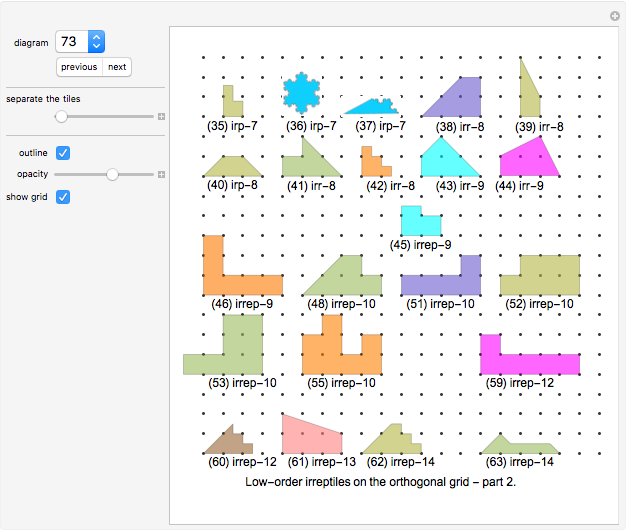
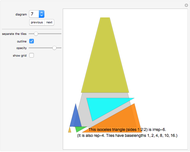
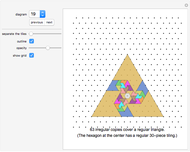
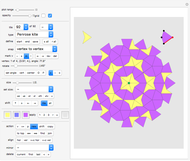
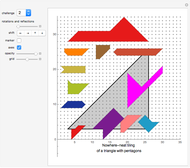
Content of this Demonstration Diagrams 1 to 63: Irregular self-tilings of irreptiles with less than 20 pieces in the tiling (irregular order less than 20).
If a shape is a polysquare such that two copies tile a rectangle, then the associated regular and irregular self-tilings are usually quite straightforward and obvious, if not trivial. Therefore some of these cases have been ignored in this Demonstration.
Additionally, overview diagrams are given:
Diagrams 64 to 70 are overview diagrams.
Diagrams 64, 65: Overviews of the irreptiles on the orthogonal grid presented in diagrams 1 to 63.
Diagrams 66, 67: Overviews of the irreptiles on the isometric (60-degree) grid presented in diagrams 1 to 63.
Diagram 68: Overview of the irreptiles on the orthogonal grid with irregular order greater than 19.
Diagram 69: Overview of the irreptiles on the isometric (60-degree) grid with irregular order greater than 19.
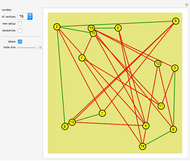
Diagram 70: A graph depicting the irregular order of some irreptiles versus their regular order.
The author conjectures that the diagonal does not have any entries.
Browse all topics
