Interactive Rings Tessellation

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
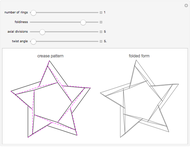
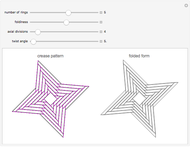
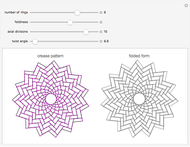
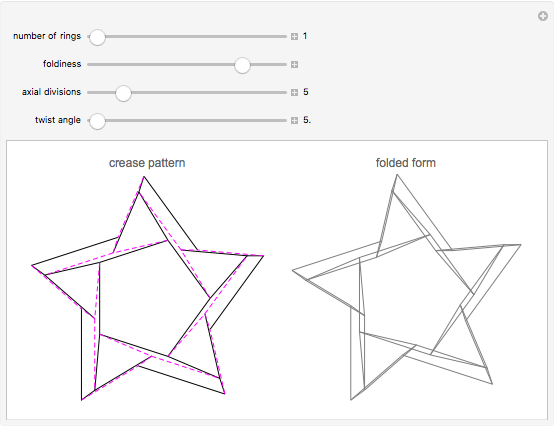
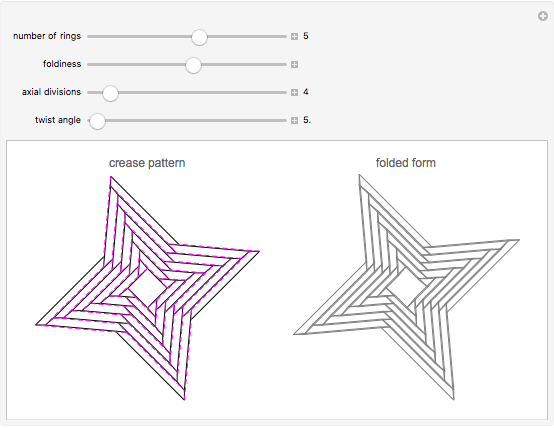
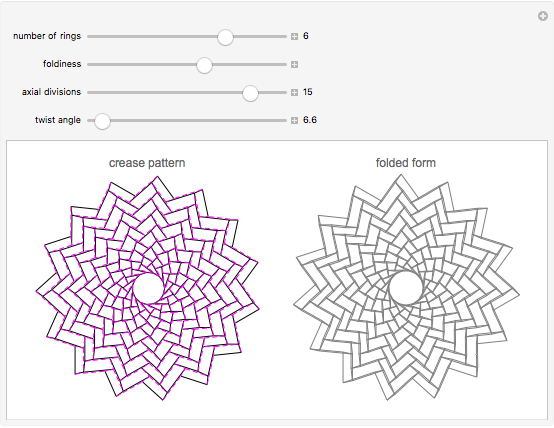
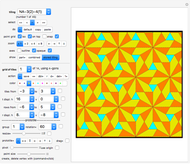
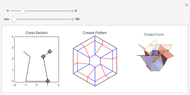
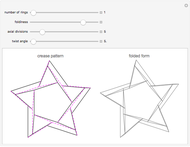
This demonstrates a rings-type origami tessellation. The left image is the crease pattern: mountain folds are solid black; valley folds are dashed magenta. The right side shows the folded form—the pattern you would get if you folded the crease pattern from translucent paper. The controls affect various parameters that define the design.
Contributed by: Robert J. Lang (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Each set of control values defines an origami tessellation, a crease pattern that when folded flat creates a geometric dissection outlined by the folded edges of the paper. Origami tessellations can be folded from opaque or translucent paper. If you use translucent paper, all folded edges and layers show through the paper, giving a pattern similar to the image shown on the right.
All of the functions necessary to create the tessellation are included in this Demonstration, and the function MakeEgg[] is the main function. It returns a list {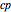 ,
,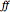 } where
} where 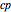 is a Graphics[] object of the crease pattern and
is a Graphics[] object of the crease pattern and  is a Graphics[] object of the folded form. If you would like to try actually folding one of these tessellations, you can extract the crease pattern from the list returned by MakeEgg[], print it separately, and/or export it to a graphics program for further manipulation.
is a Graphics[] object of the folded form. If you would like to try actually folding one of these tessellations, you can extract the crease pattern from the list returned by MakeEgg[], print it separately, and/or export it to a graphics program for further manipulation.
The functions of the controls are mostly self-evident; the "number of rings" and "axial divisions" are fairly obvious. "Foldiness" affects the size of the folded shape relative to the original crease pattern; larger values of foldiness give smaller, thicker folded forms. Each internal vertex of the crease pattern is of degree four—that is, surrounded by four lines and four angles; "twist angle" defines the smallest of those four angles (for all vertices).
Origami tessellations grew out of the traditional art of origami but have become their own standalone field. Pioneering work was done by Shuzo Fujimoto in the latter part of the 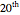 century, with significant developments from Paulo Taborda Barreto and Chris K. Palmer in the 1990s. Several construction algorithms (though not this one) and their resulting patterns may be found in the 1994 book, Origami Science and Technology, which is the proceedings of a conference on origami science and art. Since then, many artists have developed many different algorithms yielding different families of origami tessellations.
century, with significant developments from Paulo Taborda Barreto and Chris K. Palmer in the 1990s. Several construction algorithms (though not this one) and their resulting patterns may be found in the 1994 book, Origami Science and Technology, which is the proceedings of a conference on origami science and art. Since then, many artists have developed many different algorithms yielding different families of origami tessellations.
For examples of what some of these patterns look like in real paper, photographs of several folded examples may be found at the author's page. You can also find many more examples of this genre by searching for "origami tessellations" on the web and on image collection websites.
Permanent Citation