Eigenvalues and Linear Phase Portraits
Initializing live version
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
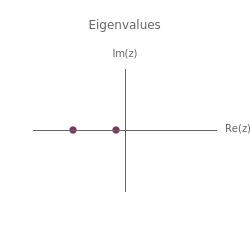
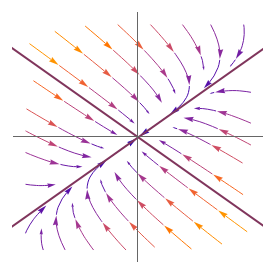
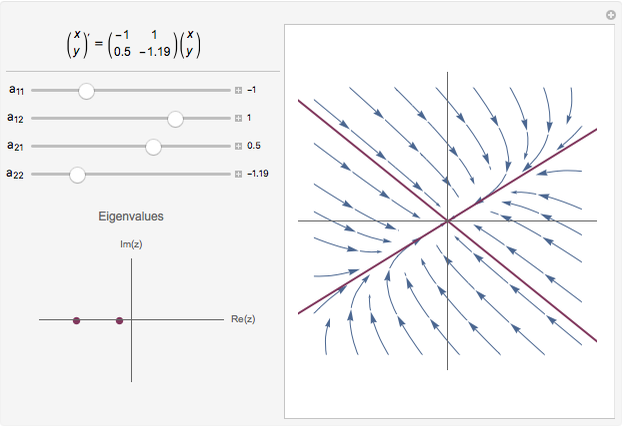
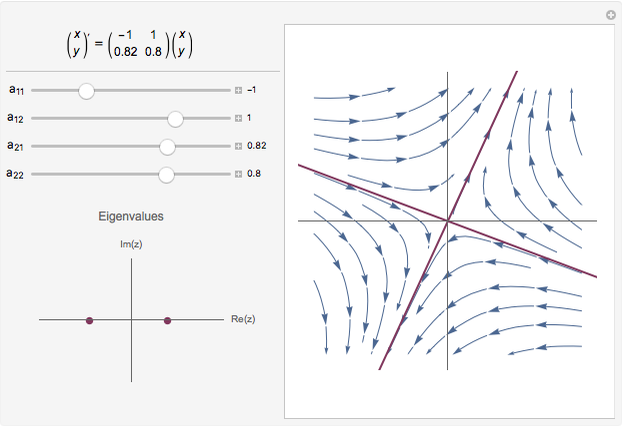
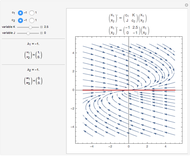
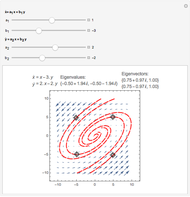
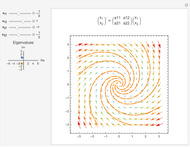
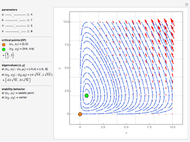
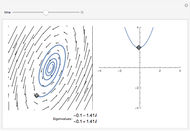
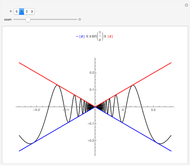
This shows the phase portrait of a 
linear differential system along with a plot of the eigenvalues of the system matrix in the complex plane.
Contributed by: Selwyn Hollis (March 2010)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Sliders allow manipulation of the matrix entries over 
. By viewing simultaneously the phase portrait and the eigenvalue plot, one can easily and directly associate phase portrait bifurcations with changes in the character of the eigenvalues.
Permanent Citation
Related Demonstrations
More by Author
Phase Portraits, Eigenvectors, and Eigenvalues
Stephen Wilkerson and Stanley Florkowski
Phase Portrait and Field Directions of Two-Dimensional Linear Systems of ODEs
Santos Bravo Yuste
Eigenfunctions and Eigenvalues of the Airy Equation Using Spectral Methods
Housam Binous, Brian G. Higgins, and Ahmed Bellagi
Using Eigenvalues to Solve a First-Order System of Two Coupled Differential Equations
Stephen Wilkerson
Phase Portrait of Lotka-Volterra Equation
Wusu Ashiribo Senapon and Akanbi Moses Adebowale
Matrix Solutions to Airy's Eigenvalue Problem
Muthuraman Chidambaram
Linear Multistep Methods Generator for First-Order ODEs
Wusu Ashiribo Senapon
Homogeneous System of Three Coupled, First-Order, Linear Differential Equations
Stephen Wilkerson
Phase Space of an Intermittently Driven Oscillator
Manu P. John and V. M. Nandakumaran
Two-Dimensional Linear Systems
Mark McClure
