Two-Dimensional Linear Systems

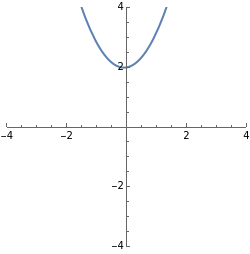
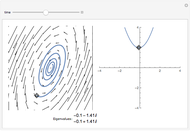
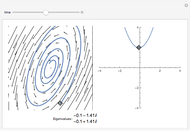
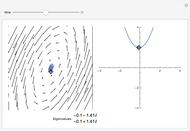
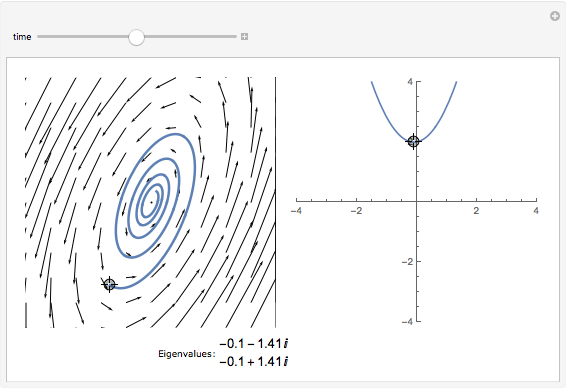
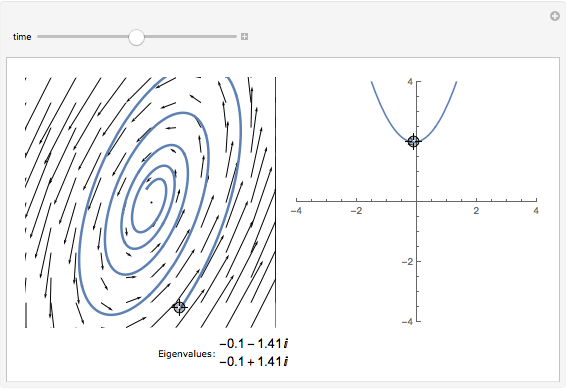
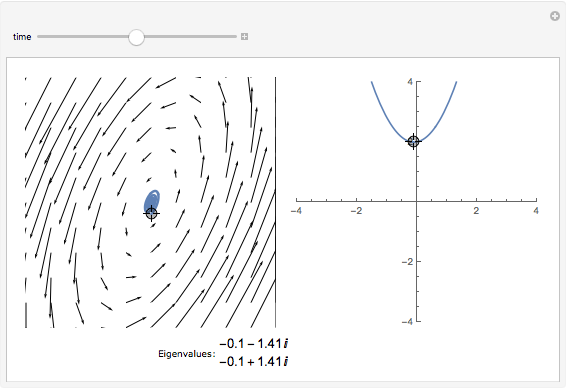
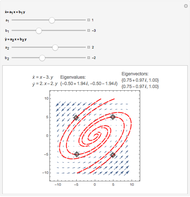
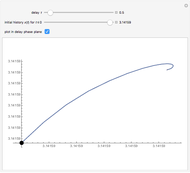
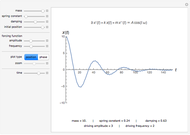
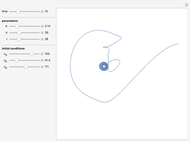
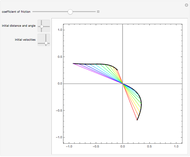
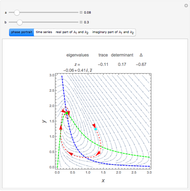
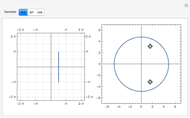
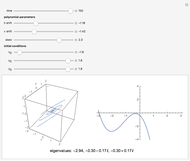
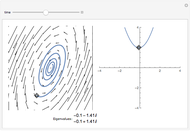
The dynamics of a system of two differential equations may be analyzed using the eigenvalues of the coefficient matrix. For example, the origin will be attractive if the real part of both eigenvalues is negative and the system will be rotational if the eigenvalues are complex. The eigenvalues are determined by the roots of the characteristic polynomial, which is the movable parabola in this Demonstration. As the parabola moves, the nature of the vector field and the path through the vector field both change. The starting location of the path may also be moved.