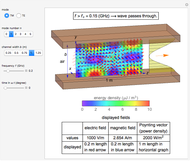
Electric and Magnetic Fields near a Transmission Line

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
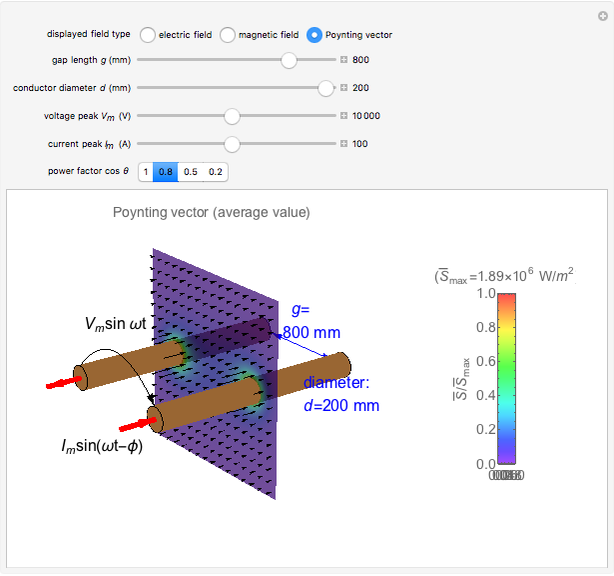
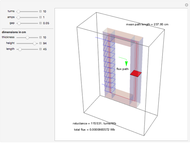
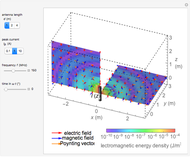
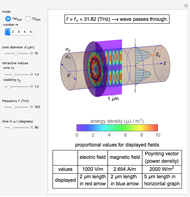
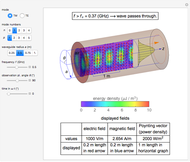
This Demonstration shows the fields in the region near a transmission line consisting of a pair of cylindrical conductors. The electric and magnetic fields and the Poynting vector distribution are shown by colors and arrows. The sinusoidal frequencies of the voltage and current are assumed to be sufficiently low for the electric and magnetic fields of the slowly changing configurations to be analyzed by assuming static behavior. You can vary the gap and cylinder diameter, as well as the voltage, current, and power factor of the transmission line.
Contributed by: Y. Shibuya (October 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
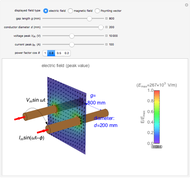
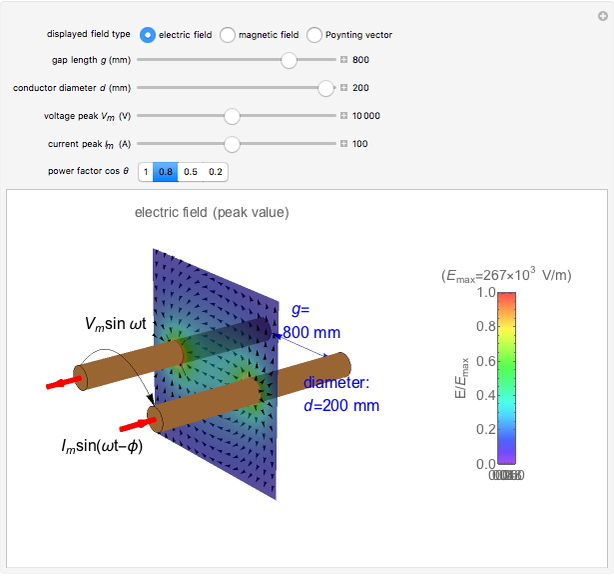
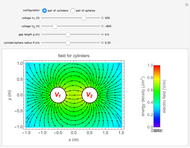
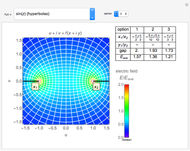
Snapshot 1: an electric field distribution
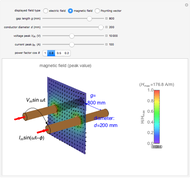
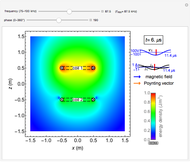
Snapshot 2: a magnetic field distributions
Snapshot 3: a Poynting vector distribution
The electric field  of parallel cylinders is calculated assuming parallel line charges with separation
of parallel cylinders is calculated assuming parallel line charges with separation 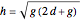 , where
, where  and
and  are the gap length and cylinder diameter. The magnetic field
are the gap length and cylinder diameter. The magnetic field 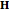 is simulated by that of parallel line currents flowing along the cylinder axes (i.e. a uniform current density is assumed, ignoring the skin effect). The electric and magnetic vectors are in the plane of observation perpendicular to the cylinders. The average of the Poynting vector, given by
is simulated by that of parallel line currents flowing along the cylinder axes (i.e. a uniform current density is assumed, ignoring the skin effect). The electric and magnetic vectors are in the plane of observation perpendicular to the cylinders. The average of the Poynting vector, given by  , is directed along the axial direction of conductors.
, is directed along the axial direction of conductors.
The electric and magnetic field intensities (shown in colors for the peak values) are similarly distributed on the observation plane, but the directions are very nearly mutually perpendicular. The Poynting vector's intensity distribution in space decreases rapidly with the distance from the conductor.
The power of the transmission line is actually carried in a thin region on the outside of the conductors, not within the lines themselves.
Reference
[1] J. A. Stratton, Electromagnetic Theory, New York: McGraw–Hill, 1941.
Permanent Citation
"Electric and Magnetic Fields near a Transmission Line"
http://demonstrations.wolfram.com/ElectricAndMagneticFieldsNearATransmissionLine/
Wolfram Demonstrations Project
Published: October 5 2012