Electromagnetic Wave Incident on a Perfect Conductor

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
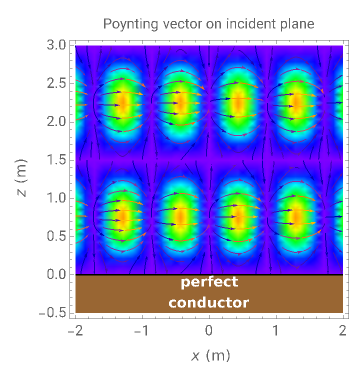
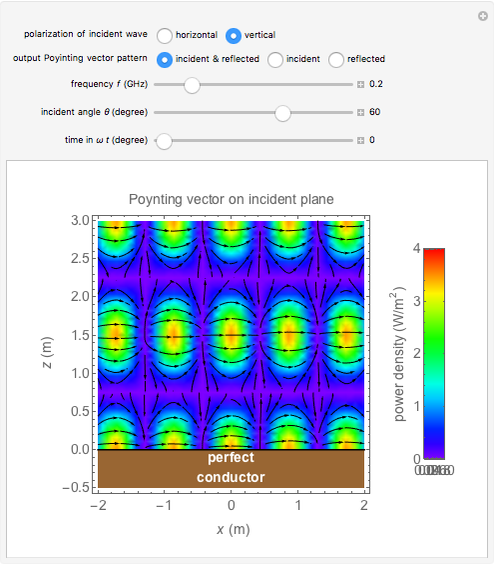
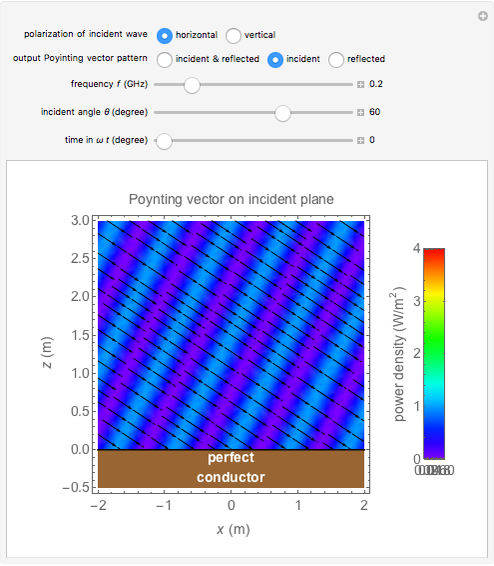
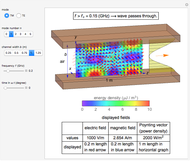
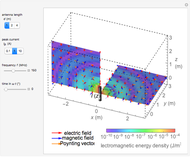
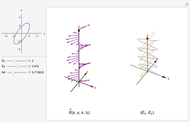
This Demonstration shows an electromagnetic wave incident on a perfect conductor calculates the corresponding Poynting vector. The incident wave is assumed to be linearly polarized in the horizontal or vertical direction (with respect to the electric field). The resulting Poynting vector pattern is shown on the incident  -
- plane. In all cases, the amplitude of the incident electric field is set to
plane. In all cases, the amplitude of the incident electric field is set to  , which corresponds to
, which corresponds to 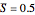 or
or 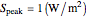 in power density.
in power density.
Contributed by: Y. Shibuya (October 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
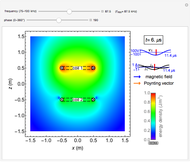
Snapshot 1: Poynting vector plot for vertically polarized incident wave at angle 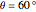
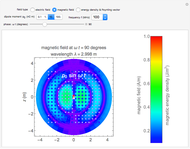
Snapshot 2: Poynting vector plot for incident wave of 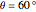 (same for horizontal or vertical waves)
(same for horizontal or vertical waves)
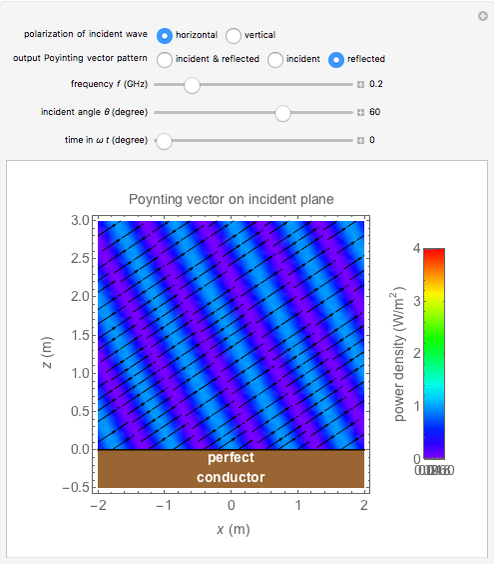
Snapshot 3: Poynting vector plot for reflected wave for incident wave of 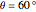 (same for horizontal or vertical waves)
(same for horizontal or vertical waves)
For the horizontally-polarized electromagnetic wave propagating along the  axis, the electric field is given by
axis, the electric field is given by 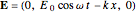 , while for the vertically-polarized wave,
, while for the vertically-polarized wave, 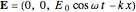 . Here,
. Here, 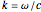 is the propagation factor. In both cases, the corresponding magnetic field is given by
is the propagation factor. In both cases, the corresponding magnetic field is given by  , where
, where 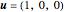 is the propagation direction, and
is the propagation direction, and 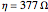 is the wave impedance.
is the wave impedance.
Similarly, the fields for the incident angle  can be determined for both incident reflected waves as
can be determined for both incident reflected waves as 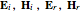 . Then the resultant fields
. Then the resultant fields  and
and 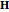 can be obtained by superposition. The Poynting vector can be calculated accordingly.
can be obtained by superposition. The Poynting vector can be calculated accordingly.
The Poynting vector pattern of the incident wave (or reflected wave) is the same whether the polarization is horizontal or vertical. However, the superposed pattern is different because the reflected wave's phase depends on the polarization.
The Poynting vector's intensity and direction are shown by colors and arrows in the output pattern. The intensity increases as  approaches 90°, and the average direction is always toward the positive
approaches 90°, and the average direction is always toward the positive  direction.
direction.
Reference
[1] D. K. Cheng, Field and Wave Electromagnetics, 2nd ed., Reading, MA: Addison-Wesley, 1989.
Permanent Citation