Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Equatorial Telescope Mounts

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

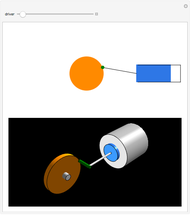
To keep an astronomical object within the field of view, telescopes need to be able to compensate for the Earth's rotation. Some telescopes use an equatorial mount, which allows the telescope to track an object along a parallel to the celestial equator. This kind of telescope mount is particularly useful for astrophotography.

[more]

The polar axis (green) is pointed at the north celestial pole; its angle to the horizon is the same as the observer's latitude. Once the telescope mount is aligned to the pole, the right ascension (r.a.) and declination (dec.) are adjusted to match the celestial coordinates of the object.

[less]

Contributed by: Jeff Bryant (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

As a result of the Earth's rotation, the right ascension coordinate drifts across the sky along a path parallel to the celestial equator. Once the telescope is adjusted to point at an object's sky coordinates (right ascension and declination), it is simply a matter of driving the right ascension axis with a motor to keep up with the object as it moves.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send