Exploring Social Choice Theory

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
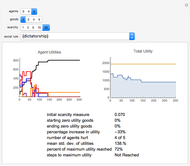
This Demonstration is devoted to understanding all combinations of five social choice systems; namely the systems of democracy, exchange, theft, oligarchy, and dictatorship. Each run examines the effects of a particular set of social rules on a society of a given number of agents and goods, and a given level of scarcity (the ratio of total goods demand to total goods available, with some random variation). The goal is to explore the effects of different social resource distribution rules on various measures of social and individual utility.
[more]
Contributed by: Earl Mitchell (March 2011)
Suggested by: Jason Cawley
Open content licensed under CC BY-NC-SA
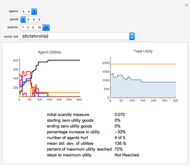
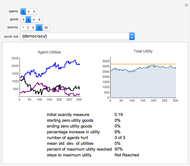
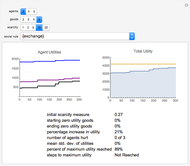
Snapshots
Details
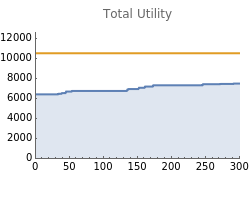
The concept of utility has been pivotal for the history of economics. In classical economics the assumption of rationality is defined by the effects of an exchange on individual utility. In welfare economics we consider the notion of "social utility"; utility aggregated across individuals. The idea of social utility goes back to the utilitarians at least—but in modern economics social utility is a simple quantitative measure of a social state not requiring any normative utilitarianism.
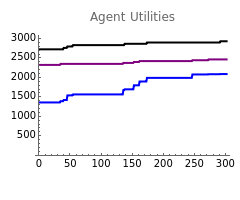
Here, utility is the determinant of social decision making. Each possible allocation of goods among possible owners has some utility for each individual as well as an aggregate utility measure across all individuals (social utility). No equalizing assumptions about demands are made in this Demonstration; agent A's demand for good X is a number—it can in principle be any number. Generally greater demands have a greater impact on overall social utility.
More specifically we need to understand the concept of "marginal utility". When an individual has no inventory, the marginal utility of that good is simply equal to their total demand for that good. Marginal utilities are then assumed to decrease linearly as goods are acquired; that is, the utility of acquiring one additional good is equal to the utility of the last good acquired minus one. When demand is saturated (when goods in inventory equal demand), the marginal utility of an additional good is assumed to be zero—or the individual is indifferent to the accumulation of surplus goods. The net result is a straight line approximation of the marginal utility function with a maximum of individual demand for the good and a minimum of zero.
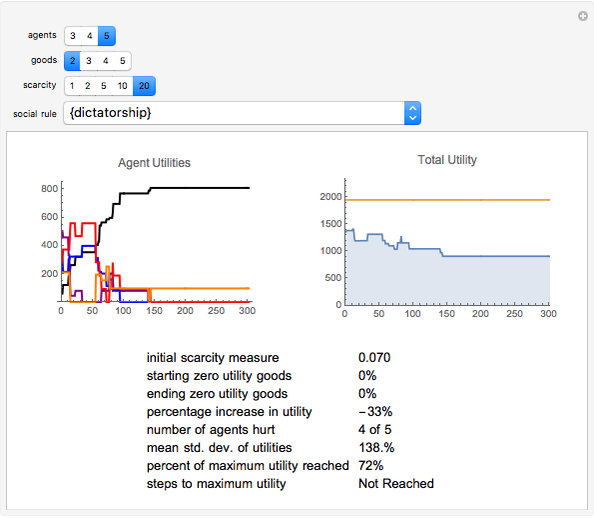
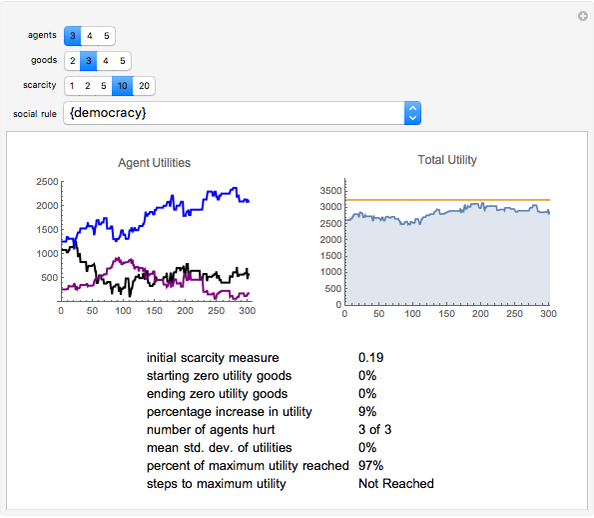
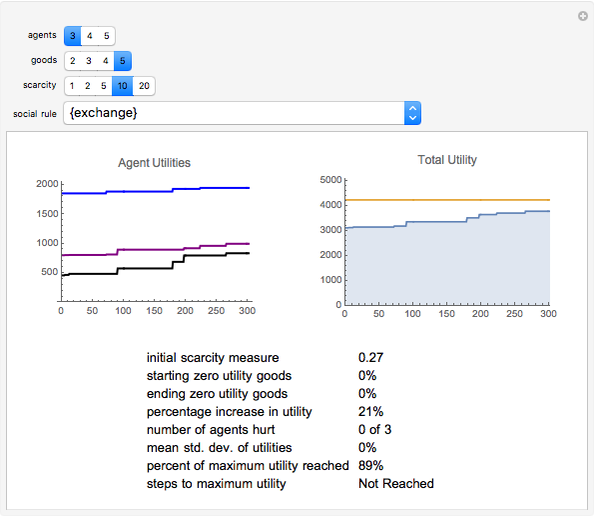
An initial condition is an initial set of demands for each agent for each good, and an initial distribution of goods among the agents (or their inventories). The social rules are the procedures for rearranging the distribution of goods, and the rearrangement of goods can be considered a proposed "trade". Each rule has a unique criterion for determining the success of the proposed trade; e.g. "exchange" means the trade occurs if all parties' utilities increase; "democracy" means the trade occurs if more than half the society's utility will increase; "theft" means the trade will occur as long as the trade proposer's utility is increased (regardless of the impact on other individual's utilities); "oligarchy" means that the trade occurs if more than half of some subset of the society's utility increases; and "dictatorship" means that the trade occurs if the utility of the dictator is increased.
For each iteration an individual is randomly selected to propose a trade. The proposed trade is then evaluated using the social choice rules selected; when more than one rule is included the rule is selected at random on each iteration. In this model the individual demands are assumed to remain constant through time so each iteration will return the original demand function and a new distribution of goods. This then becomes the social condition for the next iteration. In this way agents do not have perfect foresight for the consequences of their trades, and cannot precalculate results outside of the current iteration. These rules have been explored theoretically and mathematically by economists and mathematicians from Marquis de Condorcet to Kenneth Arrow. While formal methods for analyzing systems of social choice have been developed, there have been few studies of simulations involving computer simulated social choice. The NKS paradigm, including Stephen Wolfram's principal of computational equivalence, promotes the notion that the end behaviors of these types of systems may not be discoverable through the standard formal methods of mathematical analysis.
Several interesting behaviors are immediately observable:
1. In the absence of other social rules, "exchange" often results in a sub-optimal distribution.
2. As scarcity increases, the volatility of utility in voting systems like "democracy" increases.
3. There are situations in which any of the possible rule combinations can outperform any of the others. In other words, the performance of a given system of social choice exhibits high dependence on initial conditions.
Lastly, it is important to consider the assumptions that underly the model as they provide a guide for future investigation. The assumptions include:
1. Goods are never created or destroyed; they are only moved between agents.
2. The number of individuals is fixed for each run.
3. An individual's preferences do not change.
4. Marginal utilities decrease linearly as a function of goods owned, from a maximum of total demand for the good with a minimum of zero.
5. The utilities of all goods are independent and additive (absence of complementarity).
6. All surplus goods (goods in excess of demands) have utility zero.
Permanent Citation
"Exploring Social Choice Theory"
http://demonstrations.wolfram.com/ExploringSocialChoiceTheory/
Wolfram Demonstrations Project
Published: March 7 2011