Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Fibonacci Rabbits

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

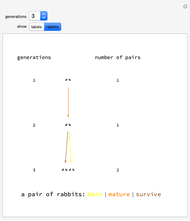
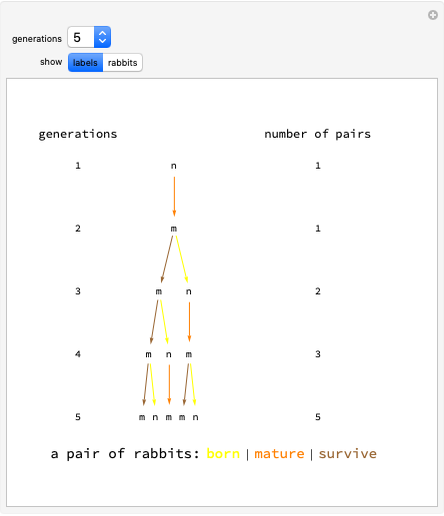
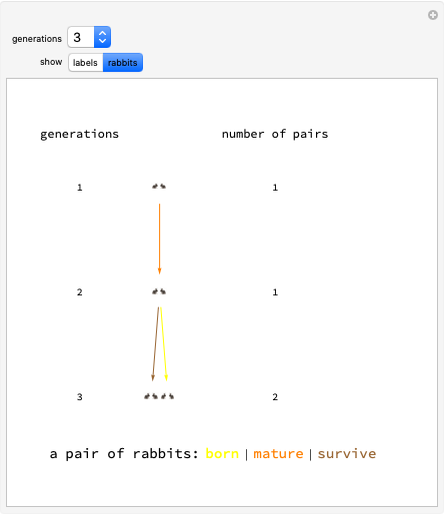
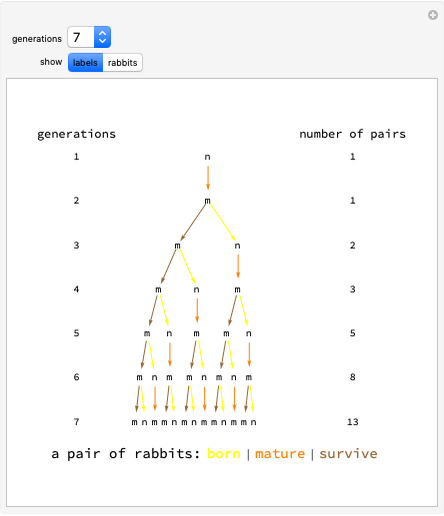
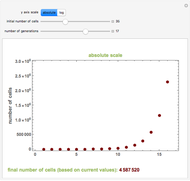
In 1202 Fibonacci investigated how fast rabbits could breed.

[more]

Suppose a pair of rabbits, one male and one female, start a family. Rabbits mature at the age of one month (labeled "m") and a female produces a new pair of rabbits (labeled "n") at the end of its second month.

Suppose that the rabbits survive forever and that a female always produces one new pair (one male, one female) every month, giving the original pair and a new one.

How many pairs will there be in eight generations?

[less]

Contributed by: Enrique Zeleny (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

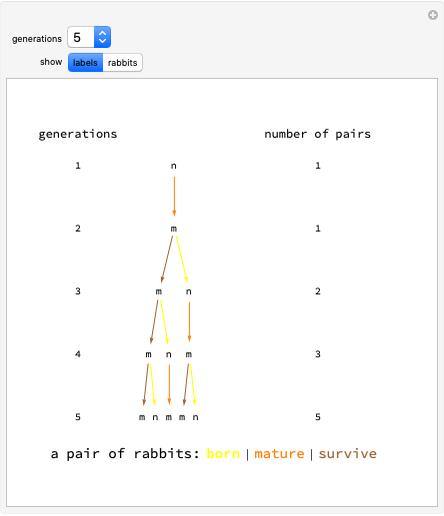
The sequence can be reproduced by a substitution system, replacing every "m" in one month by "mn" in the next and similarly replacing every "n" by "m".

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send