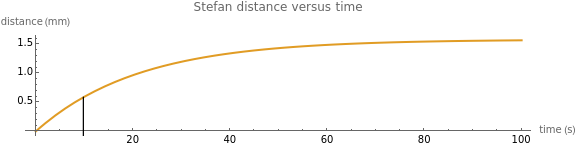
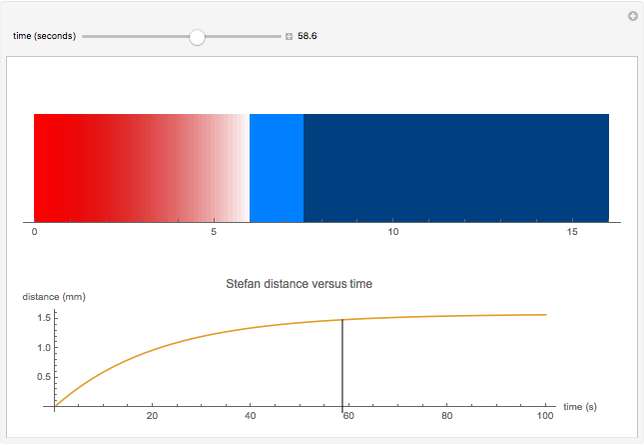
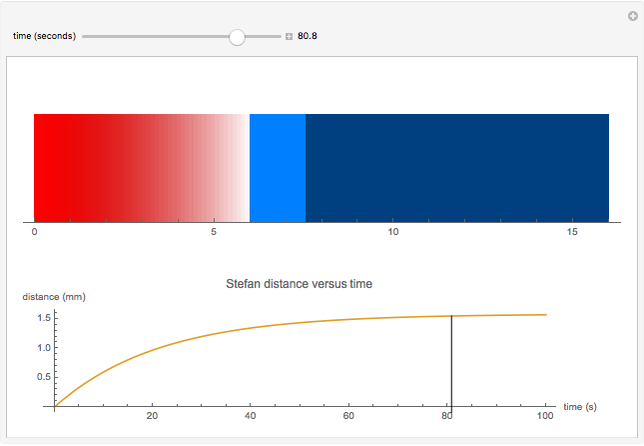
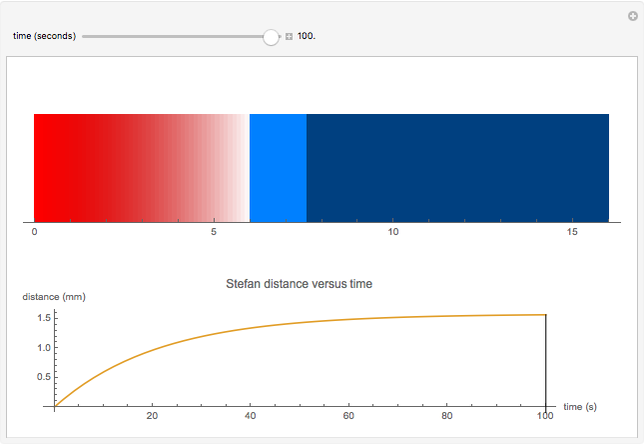
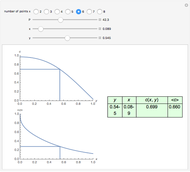
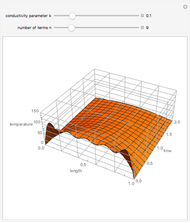
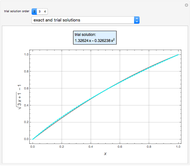
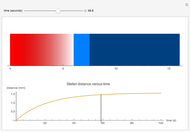
A Stefan problem is a type of boundary value problem in which a phase boundary can move with time. A first-order approximation of the Stefan problem is explored for a system consisting of a block of ice (0° C) attached to a 6 mm thick piece of glass pulled from boiling water at 100° C. Here the Stefan problem is simplified by assuming that the temperature of the glass decreases linearly across the glass from 100° C at the left edge to 0° C at the glass-ice interface, as indicated by the color gradient. As time progresses, heat flows from the glass into the water composite at a rate proportional to the temperature gradient of the glass. The heat entering the frozen ice melts a water layer. The thickness of the water is plotted as a function of time.