Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Tracking the Frank-Kamenetskii Problem

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

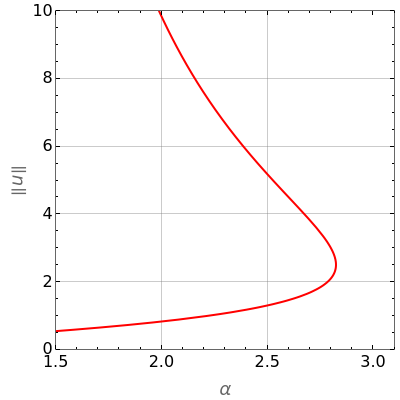
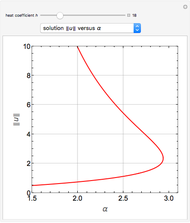
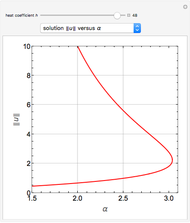
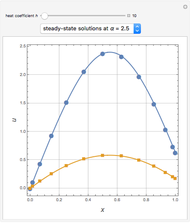
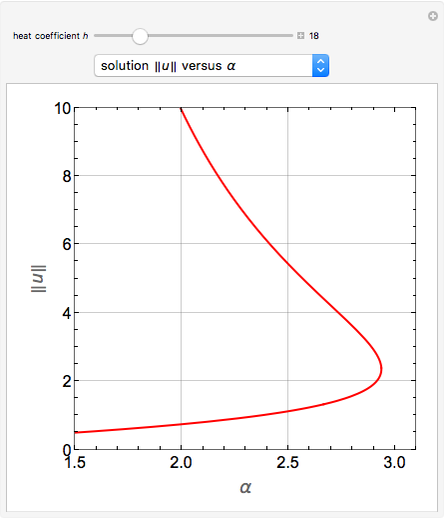
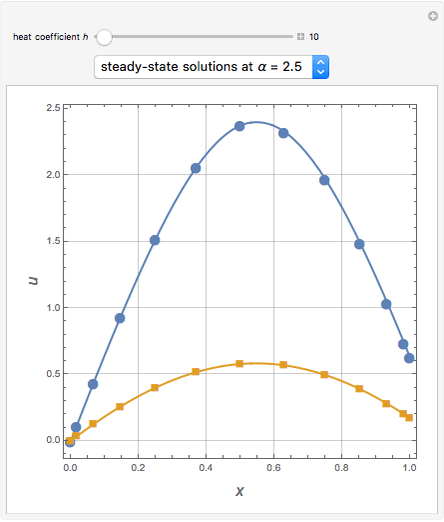
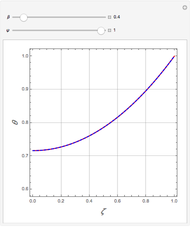
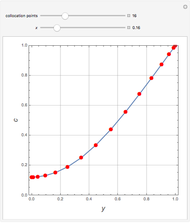
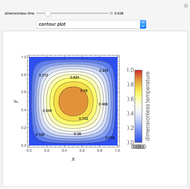
The Frank–Kamenetskii problem relates to the self-heating of a reactive solid. When the heat generated by reaction is balanced by conduction in a one-dimensional slab of combustible material, the nonlinear boundary value problem (BVP) for , , and admits up to two solutions. Here, is the dimensionless temperature and is the heat transfer coefficient.

[more]

For and , the BVP admits an analytical solution given by , where is one of the two solutions of the transcendental equation (i.e., and ).

We use the homotopy continuation method and the Chebyshev orthogonal collocation technique (with collocation points) to track the solutions, , in the parameter space.

The plot of the norm of the solution versus clearly indicates that there can be up to two solutions. These two solutions are plotted in blue and magenta for .

[less]

Contributed by: Housam Binousand Brian G. Higgins (May 2013)
Open content licensed under CC BY-NC-SA

Snapshots

Details

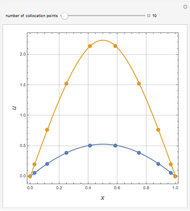
In the discrete Chebyshev–Gauss–Lobatto case, the interior points are given by . These points are extremums of the Chebyshev polynomial of the first kind .

The Chebyshev derivative matrix at the quadrature points , , is given by

, , for , and for , , and ,

where for and .

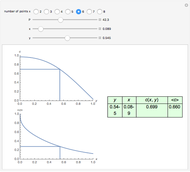
The matrix is then used as follows: and , where is a vector formed by evaluating at , , and and are the approximations of and at the .

References

[1] P. Moin, Fundamentals of Engineering Numerical Analysis, Cambridge, UK: Cambridge University Press, 2001.

[2] L. N. Trefethen, Spectral Methods in MATLAB, Philadelphia: SIAM, 2000.

[3] B. G. Higgins and H. Binous, "A Simple Method for Tracking Turning Points in Parameter Space," Journal of Chemical Engineering of Japan, 43(12), 2010 pp. 1035–1042. doi:10.1252/jcej.10we122.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send