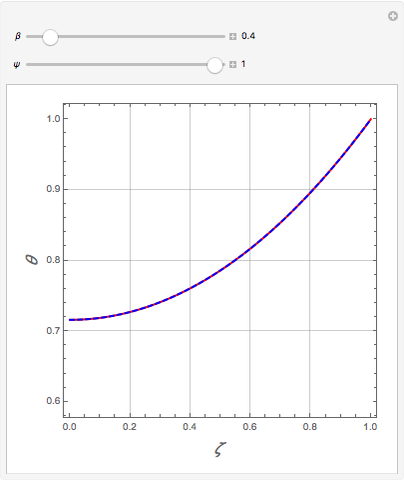
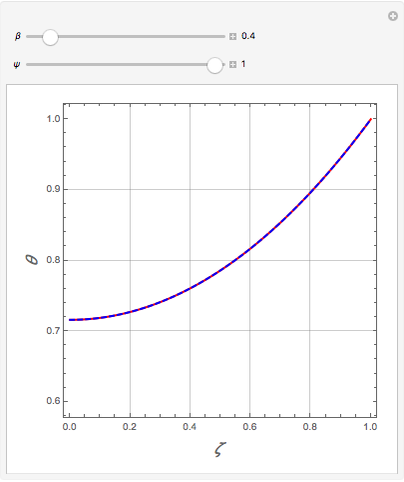
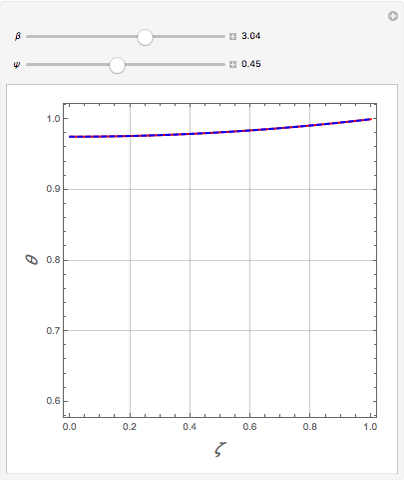
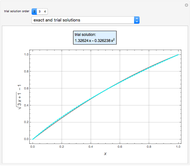
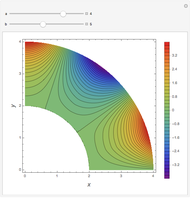
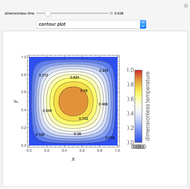
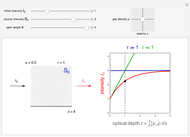
Temperature Distribution in Convective Fins with Variable Thermal Conductivity

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
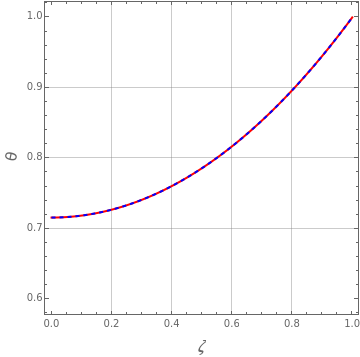
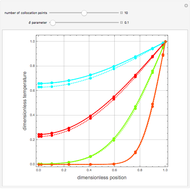
Consider a convective straight fin with temperature-dependent thermal conductivity. The dimensionless problem reduces to (see [4] for details) 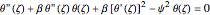 with
with 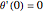 ,
, 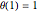 , where the dimensionless quantities and parameters are defined as follows:
, where the dimensionless quantities and parameters are defined as follows: 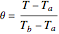 ,
,  ,
, 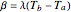 , and
, and 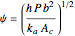 .
.
Contributed by: Housam Binous, Ahmed Bellagi, and Brian G. Higgins (September 2013)
Open content licensed under CC BY-NC-SA
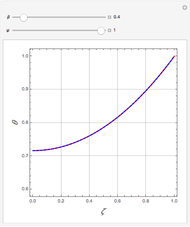
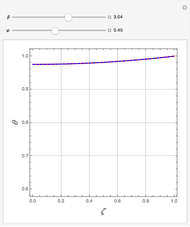
Snapshots
Details
The  -order Taylor series expansion function of
-order Taylor series expansion function of 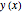 is of the form
is of the form 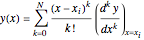 . At
. At 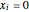 , this is the Maclaurin series,
, this is the Maclaurin series, 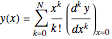 . The differential transformation
. The differential transformation 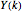 of the function
of the function 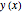 is given by
is given by 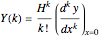 . The differential inverse transform of
. The differential inverse transform of 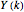 is defined by
is defined by 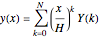 . Table 1 in [2] gives a list of properties of the differential transformation. For instance, if
. Table 1 in [2] gives a list of properties of the differential transformation. For instance, if  then
then  . In this Demonstration,
. In this Demonstration,  and
and  .
.
References
[1] M. J. Jang, C. L. Chen, and Y. C. Liu, "Analysis of the Response of a Strongly Nonlinear Damped System Using a Differential Transformation Technique," Applied Mathematics and Computation, 88(2–3), 1997 pp. 137–151. doi: 10.1016/S0096-3003(96)00308-6.
[2] C. L. Chen and Y. C. Liu, "Solution of Two-Boundary-Value Problems Using the Differential Transformation Method," Journal of Optimization Theory and Applications, 99(1), 1998 pp. 23–35. doi: 10.1023/A:1021791909142.
[3] M. J. Jang, C. L. Chen, and Y. C. Liu, "On Solving the Initial-Value Problems Using the Differential Transformation Method," Applied Mathematics and Computation, 115(2–3), 2000 pp. 145–160. doi: 10.1016/S0096-3003(99)00137-X.
[4] A. A. Joneidi, D. D. Ganji, and M. Babaelahi, "Differential Transformation Method to Determine Fin Efficiency of Convective Straight Fins with Temperature Dependent Thermal Conductivity," International Communications in Heat and Mass Transfer, 36(7), 2009 pp. 757–62. doi: 10.1016/j.icheatmasstransfer.2009.03.020.
Permanent Citation