Repeating Continued Fractions

Additional Information:

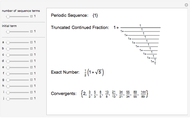
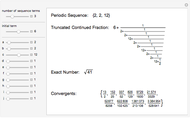
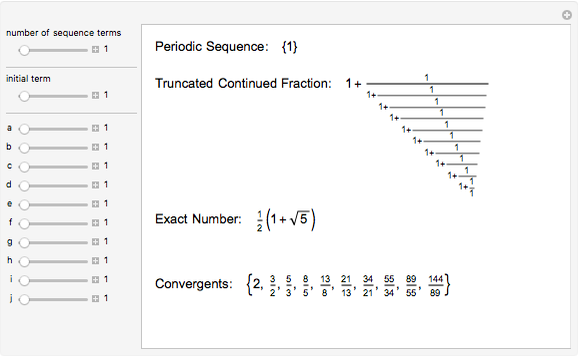
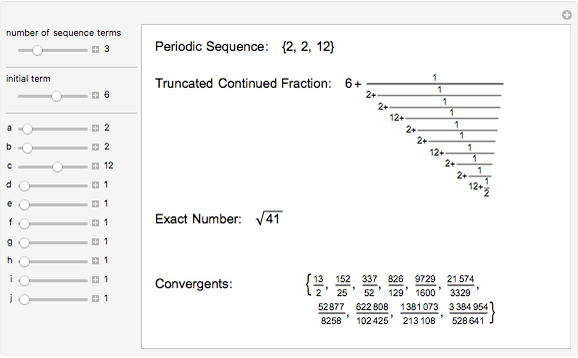
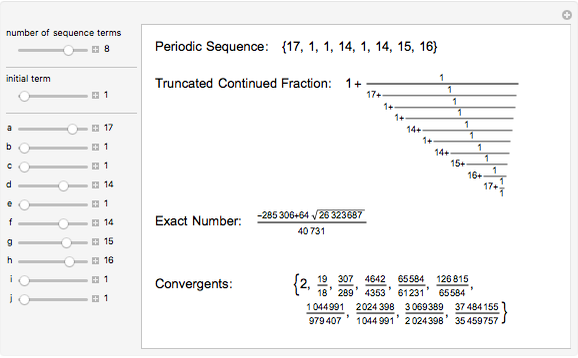
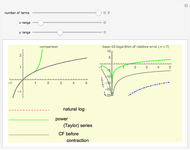
The continued fraction expansions of the square roots of the integers that are not perfect squares possess the so-called "palindromic property". That means that their periodic element sequences without the last element are palindromic (i. e., can be reversed), and the last element is twice the initial term. For example, the continued fraction expansion of 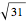is {5, {1, 1, 3, 5, 3, 1, 1, 10}}. The sequence 1, 1, 3, 5, 3, 1, 1 is palindromic, and the 10 is two times the initial 5.

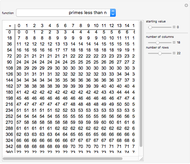
The following shows this for the first 200 integers:

DeleteCases[ContinuedFraction@Sqrt@Range@200, {_}]

http://www.joma.org/mathDL/22/?pa=content&sa=viewDocument&nodeId=3154

For more, see A Tail of Two Palindromes.