Heilbronn Triangles in the Unit Square

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
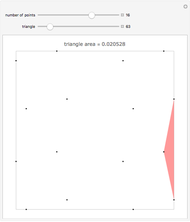
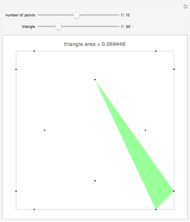
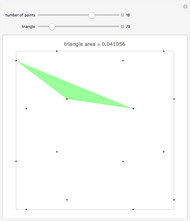
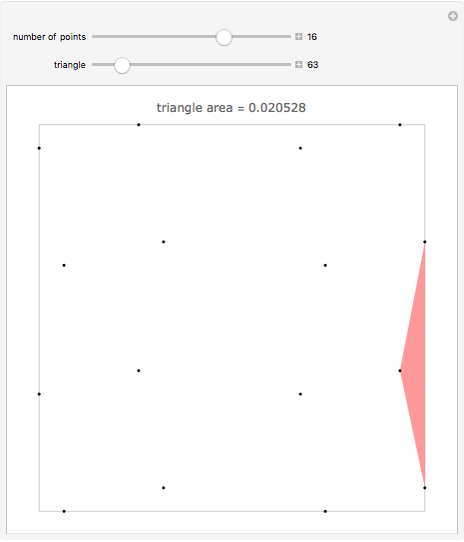
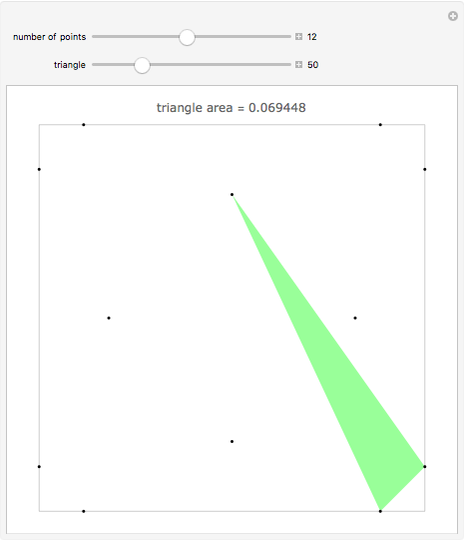
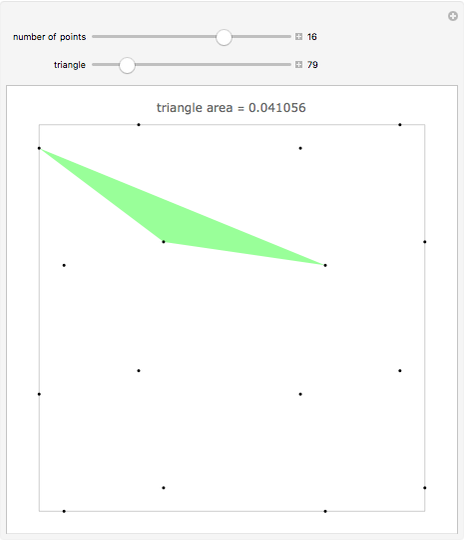
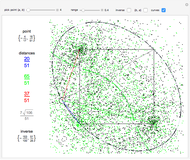
For  points in a square of side length one, find the three points that make the triangle with minimal area. Finding the placement of
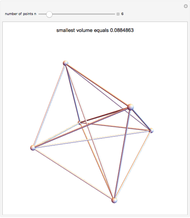
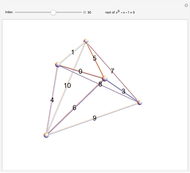
points in a square of side length one, find the three points that make the triangle with minimal area. Finding the placement of  points that produces the largest such triangle is known as the Heilbronn triangle problem. The point placements within this Demonstration are the best known. Minimal triangles are colored red. All solutions above 12 points are due to Peter Karpov (13,15), Mark Beyleveld (14,16) and Asenath Tal (17-22), with some optimization and exact solutions found by Mathematica.
points that produces the largest such triangle is known as the Heilbronn triangle problem. The point placements within this Demonstration are the best known. Minimal triangles are colored red. All solutions above 12 points are due to Peter Karpov (13,15), Mark Beyleveld (14,16) and Asenath Tal (17-22), with some optimization and exact solutions found by Mathematica.
Contributed by: Ed Pegg Jr (September 2007)
Open content licensed under CC BY-NC-SA
Details
References
[1] Erich Friedman, The Heilbronn Problem for Squares, stetson.edu/~efriedma/heilbronn/.
[2] Asenath Tal, Algorithms for Heilbronn’s Triangle Problem, 2009, cs.technion.ac.il/users/wwwb/cgi-bin/tr-info.cgi/2009/MSC/MSC-2009-08.
[3] Peter Karpov, Notable Results, 2018, inversed.ru/Ascension.htm#results.
[4] F. Comellas and J. Yebra, New lower bounds for Heilbronn numbers, 2002, combinatorics.org/Volume_9/PDF/v9i1r6.pdf.
Snapshots
Permanent Citation