GL(2,p) and GL(3,3) Acting on Points
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
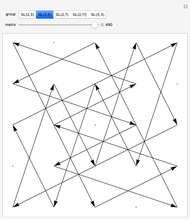
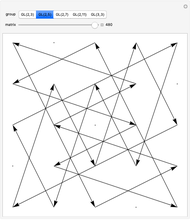
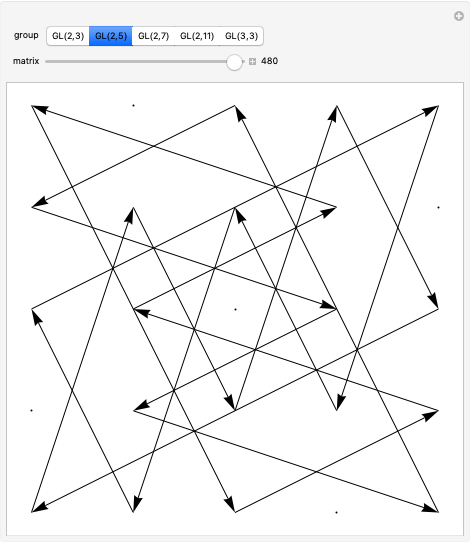
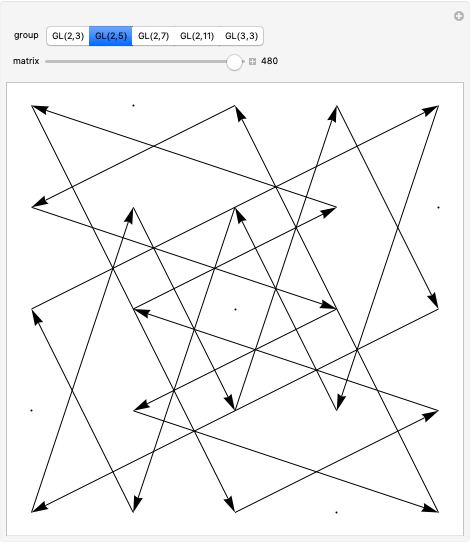
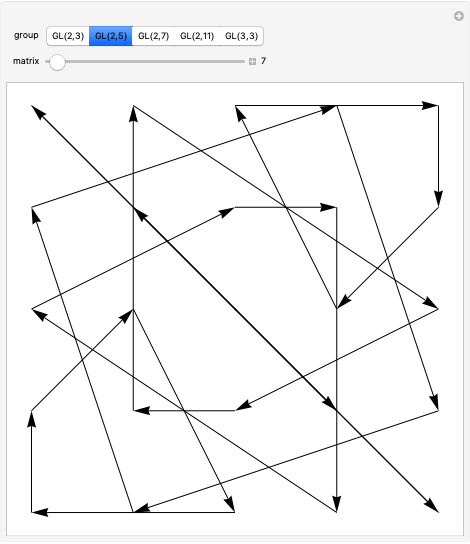
The two-dimensional space  contains nine points: (0,0), (0,1), (0,2), (1,0), (1,1), (1,2), (2,0), (2,1), and (2,2). The 48 invertible 2×2 matrices over
contains nine points: (0,0), (0,1), (0,2), (1,0), (1,1), (1,2), (2,0), (2,1), and (2,2). The 48 invertible 2×2 matrices over 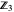 form the general linear group known as
form the general linear group known as 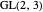 . They act on
. They act on 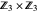 by matrix multiplication modulo 3, permuting the nine points. More generally,
by matrix multiplication modulo 3, permuting the nine points. More generally, 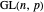 is the set of invertible
is the set of invertible  matrices over the field
matrices over the field 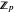 , where
, where 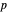 is prime
is prime With (0,0) shifted to the center, the matrix actions on the nine points make symmetrical patterns.
With (0,0) shifted to the center, the matrix actions on the nine points make symmetrical patterns.
Contributed by: Ed Pegg Jr (November 2007)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation