Generating 3D Figures with a Given Symmetry Group

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
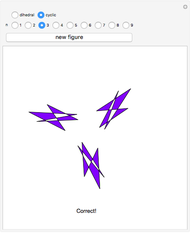
A symmetry of a figure is a transformation, such as a rotation, reflection, inversion, etc., that repositions the figure to be indistinguishable from the original. For example, rotating a circle about its center is a symmetry of the circle.
[more]
Contributed by: Izidor Hafner (December 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
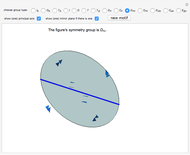
If the figure has only one rotational axis, there are the four possible kinds of symmetries, all cyclic: 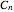 (there is an axis of rotation and reflection, but there is no mirror plane),
(there is an axis of rotation and reflection, but there is no mirror plane), 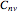 (there is a mirror plane, but it is not perpendicular to the axis),
(there is a mirror plane, but it is not perpendicular to the axis), 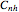 (there is a mirror plane that is perpendicular to the axis), and
(there is a mirror plane that is perpendicular to the axis), and 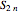 (there is a glide reflection).
(there is a glide reflection).
If the figure has more than one rotational axis but no more than one  -fold axis with
-fold axis with 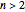 , the possibilities are (dihedral symmetries):
, the possibilities are (dihedral symmetries): 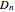 (no mirror plane),
(no mirror plane),  (the mirror plane is not perpendicular to the principal axis),
(the mirror plane is not perpendicular to the principal axis),  (the mirror plane is perpendicular to the principal axis).
(the mirror plane is perpendicular to the principal axis).
The figure may have more than one 5-fold axis (icosahedral symmetry): 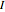 (rotations only),
(rotations only), 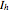 (there is a mirror plane).
(there is a mirror plane).
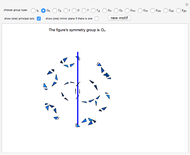
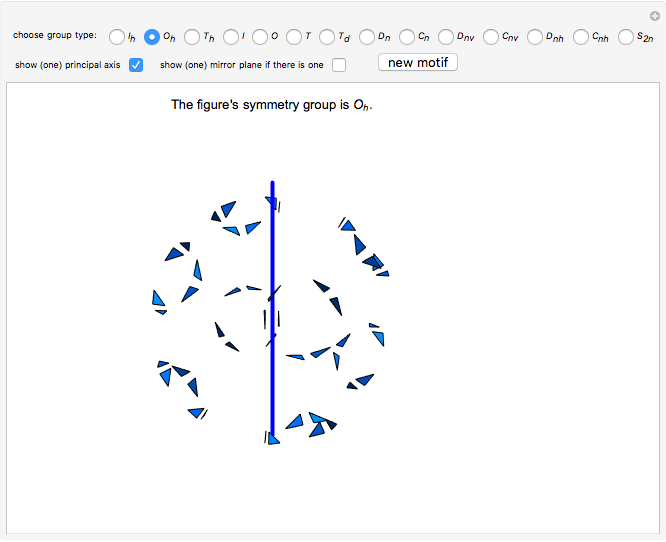
The figure may have more than one 4-fold axis (octahedral symmetry): 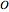 (rotations only),
(rotations only),  (there is a mirror plane).
(there is a mirror plane).
The figure may have more than one principal 3-fold axis (tetrahedral symmetry):  (rotations only),
(rotations only), 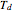 (there is a mirror plane, no inversion),
(there is a mirror plane, no inversion), 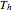 (there is a point of inversion).
(there is a point of inversion).
This Demonstration is a guessing game to learn about the 14 types of symmetry groups of figures that have a rotational axis.
Not demonstrated are the three symmetry groups with no rotational symmetry:  (asymmetric ),
(asymmetric ), 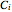 (only inversion), and
(only inversion), and 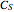 (only one mirror plane).
(only one mirror plane).
Reference
[1] P. R. Cromwell, Polyhedra, New York: Cambridge University Press, 1999 pp. 289–313. www.liv.ac.uk/~spmr02/book/index.html.
Permanent Citation