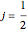Quantum Angular Momentum Matrices

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
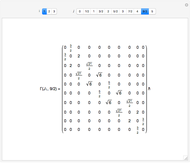
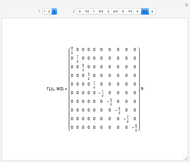
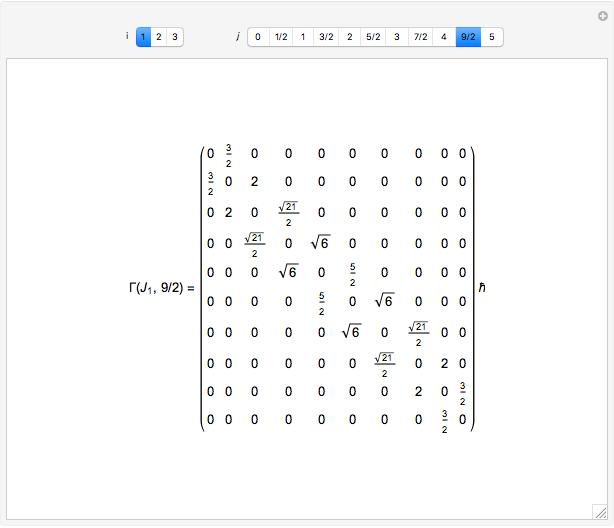
It is useful to have matrix representations of angular momentum operators for any quantum number 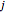 . Matrix representations can be used, for example, to model the spectrum of a rotating molecule [1].
. Matrix representations can be used, for example, to model the spectrum of a rotating molecule [1].
Contributed by: Brad Klee (January 2016)
Open content licensed under CC BY-NC-SA
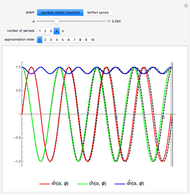
Snapshots
Details
Quantum mechanics uses the commutator
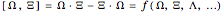
as a definitive utility. Define angular momentum as the pseudo-vector quantity 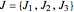 that satisfies
that satisfies
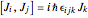 ,
,
where  is a scale factor with dimensions of action and
is a scale factor with dimensions of action and 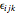 is the Levi–Civita tensor of rank three. The commutator for the
is the Levi–Civita tensor of rank three. The commutator for the 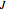 operators also defines the Lie algebra
operators also defines the Lie algebra 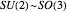 [2].
[2].
The 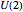 algebra describes the gauge symmetry of the 2D quantum harmonic oscillator (QHO) and admits
algebra describes the gauge symmetry of the 2D quantum harmonic oscillator (QHO) and admits 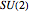 as a subalgebra, so it is possible to write the angular momentum operators in terms of the Pauli matrices
as a subalgebra, so it is possible to write the angular momentum operators in terms of the Pauli matrices 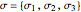 and bilinear combinations of the
and bilinear combinations of the 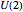 creation/annihilation operators
creation/annihilation operators 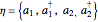 . Specifically,
. Specifically,
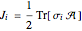 ,
,
with
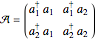 ,
,
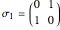 ,
, 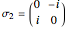 ,
, 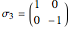 .
.
The simple 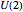 commutation relations
commutation relations
 ,
,
lead to a simple set of basis vectors, say 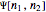 , with
, with 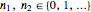 , which are also the eigenfunctions of the operator
, which are also the eigenfunctions of the operator
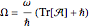 ,
,
the Hamiltonian of the 2D QHO in frequency dimensions. After we know how the  variables act on the basis vectors
variables act on the basis vectors 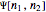 , it is possible to determine the matrix elements of any function
, it is possible to determine the matrix elements of any function 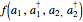 in the basis provided by
in the basis provided by 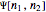 so long as the function
so long as the function 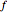 can be expanded in a power series of the noncommuting variables. Fortunately, the
can be expanded in a power series of the noncommuting variables. Fortunately, the 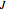 operators have only quadratic terms, which makes explicit calculation of matrix elements easy.
operators have only quadratic terms, which makes explicit calculation of matrix elements easy.
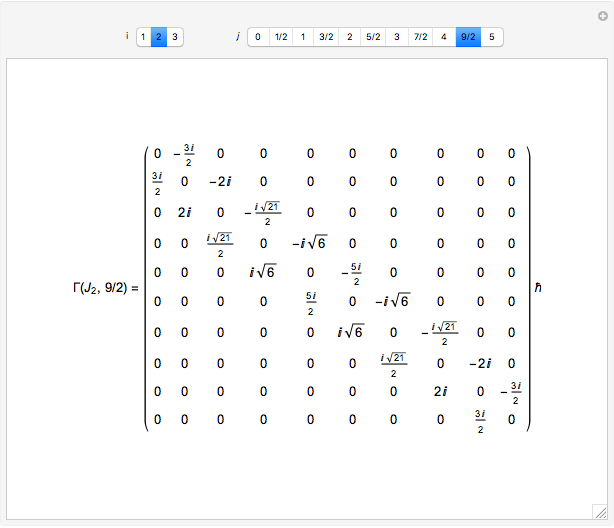
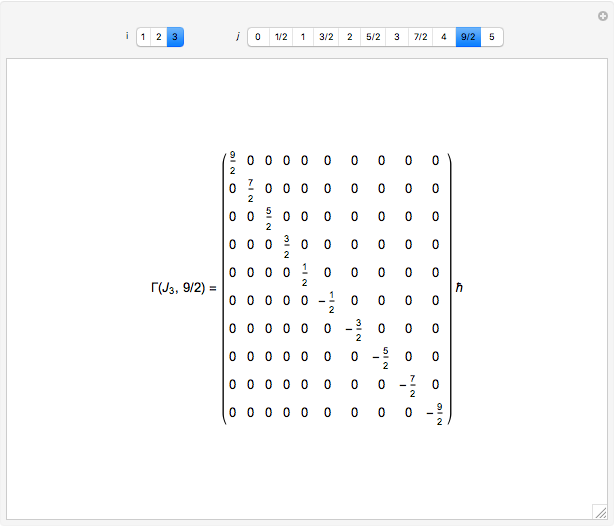
The angular momentum operators 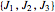 have another, more natural set of quantum numbers:
have another, more natural set of quantum numbers: 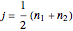 ,
,  . Each integer or half-integer
. Each integer or half-integer 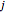 indexes an irreducible representation of the angular momentum algebra. Then we construct the irreducible representations
indexes an irreducible representation of the angular momentum algebra. Then we construct the irreducible representations 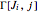 by taking the block diagonal subspace spanned by the basis vectors
by taking the block diagonal subspace spanned by the basis vectors 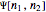 that also have quantum number
that also have quantum number 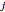 . In the usual representation where
. In the usual representation where 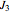 is diagonal, the
is diagonal, the 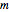 eigenvalues of representation
eigenvalues of representation 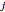 range from
range from 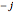 to
to 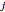 .
.
References
[1] W. Harter, "Principles of Symmetry, Dynamics, and Spectroscopy", Wiley, 1993. http://www.uark.edu/ua/modphys/markup/PSDS_Info.html
[2] F. Iachello, "Lie Algebras and Applications", Springer, 2014. http://link.springer.com/book/10.1007%2 F3-540-36239-8
[3] J. Schwinger, "On Angular Momentum," Cambridge: Harvard University, Nuclear Development Associates, Inc., 1952. www.osti.gov/accomplishments/documents/fullText/ACC0111.pdf, www.ifi.unicamp.br/~cabrera/teaching/paper_schwinger.pdf.
Permanent Citation