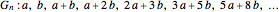Generalized Fibonacci Sequence and the Golden Ratio

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
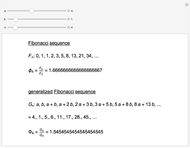
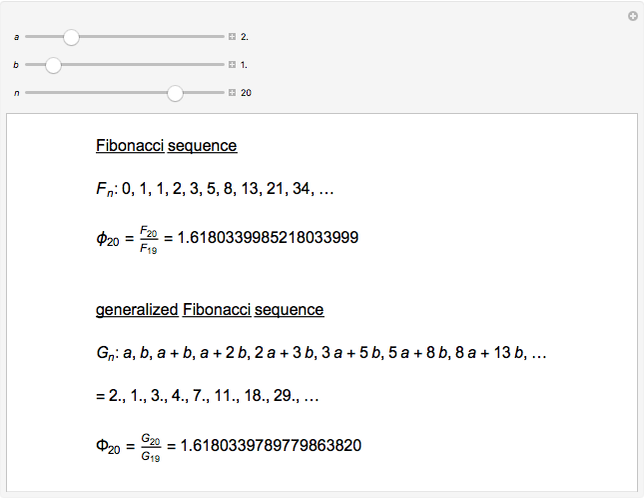
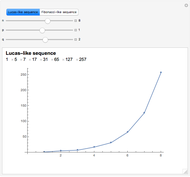
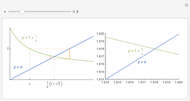
The sequence of Fibonacci numbers is given by 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …, in which each number is the sum of the two preceding numbers. As  , the ratio
, the ratio  approaches
approaches 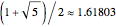 , known as the golden ratio (or golden section or divine proportion), designated by
, known as the golden ratio (or golden section or divine proportion), designated by  .
.
Contributed by: S. M. Blinder (July 2018)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Consider the original Fibonacci sequence: divide the recursion relation 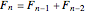 by
by 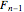 to give
to give
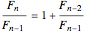 .
.
With some work, you can prove that the ratios form a Cauchy sequence, so the sequence has a limit; call it  . Thus
. Thus
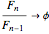
while
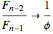 .
.
This gives 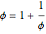 or
or 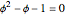 , a quadratic equation with roots
, a quadratic equation with roots
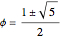 .
.
The positive root
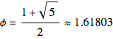
gives the golden ratio.
For the generalized Fibonacci sequence 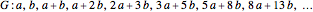 , the general term can be written using Fibonacci numbers as
, the general term can be written using Fibonacci numbers as 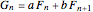 . Therefore,
. Therefore,
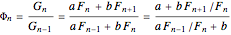 .
.
In the limit 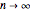 , this approaches
, this approaches
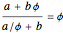 ,
,
independent of  or
or  , as long as not both are zero.
, as long as not both are zero.
Permanent Citation