Inelastic Collisions of Two Rough Spheres

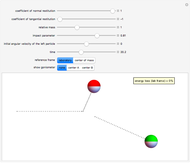
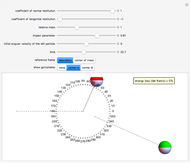
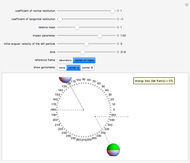
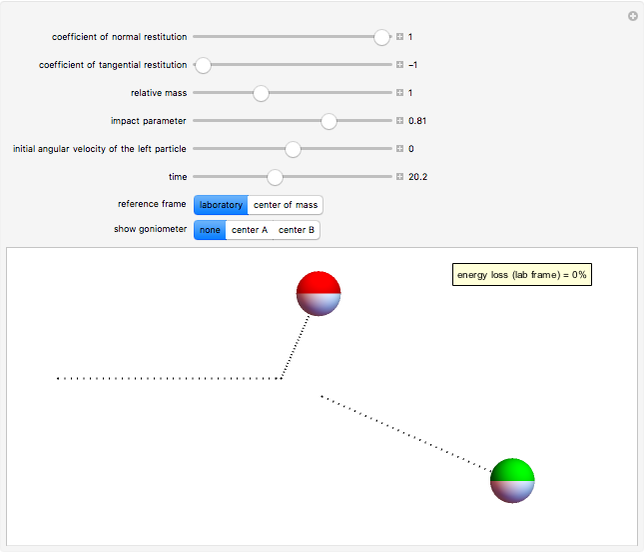
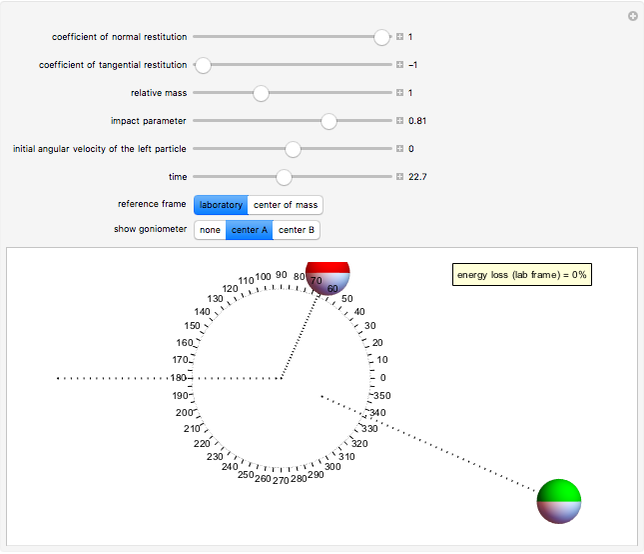
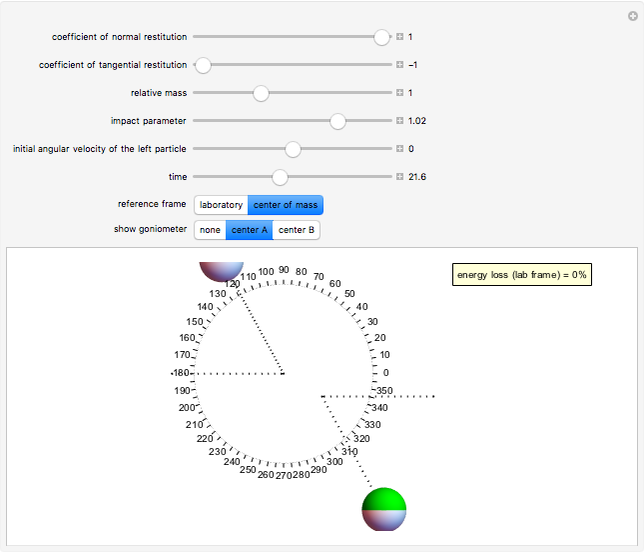
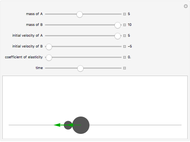
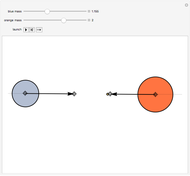
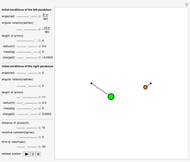
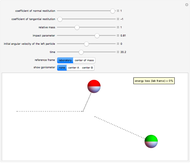
This Demonstration models inelastic collisions between two rough hard spheres of equal uniform density. You can vary the coefficient of normal restitution , the coefficient of tangential restitution 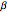, the relative mass 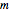, the impact parameter , and the initial angular velocity of the sphere moving from the left (the sphere rotates about an axis perpendicular to the collision plane). The coefficient of normal restitution ranges from (a perfectly inelastic collision) to (a perfectly elastic collision), while the coefficient of tangential restitution ranges from (in which the spheres are perfectly smooth) to (in which the spheres are perfectly rough). 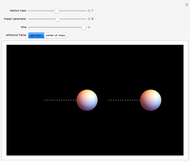The total kinetic energy is conserved only if and either or . You can observe the collision in slow motion in either the laboratory or the center-of-mass frame of reference. The spheres leave dotted contrails to help you trace their trajectories.