Plots of Quantum Probability Density Functions in the Hydrogen Atom

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
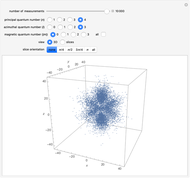
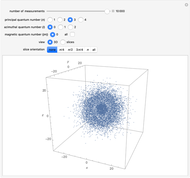
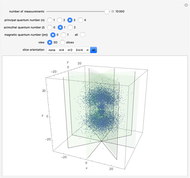
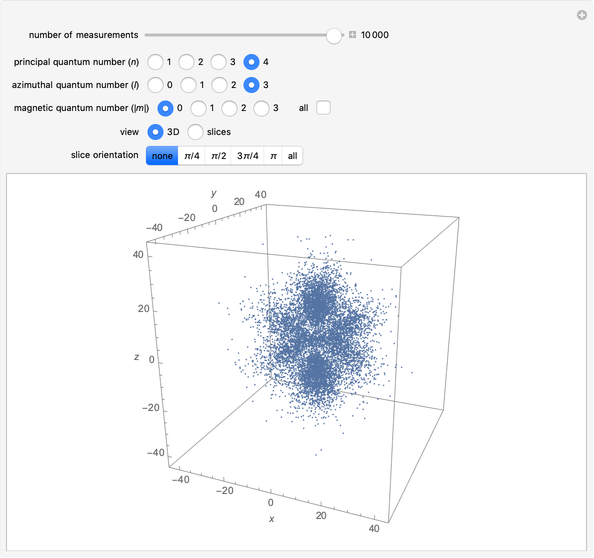
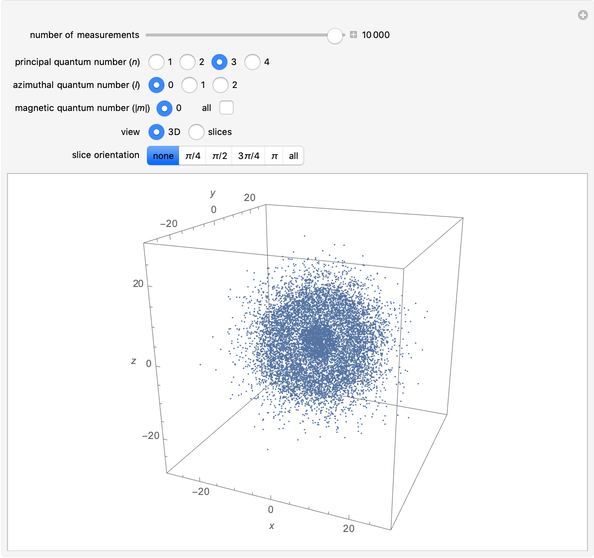
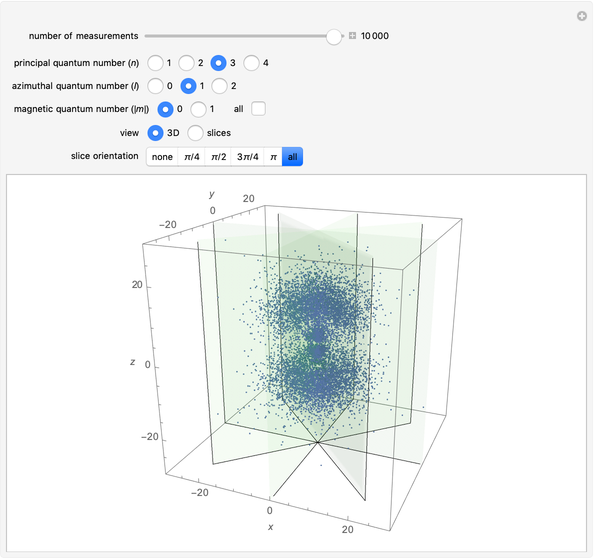
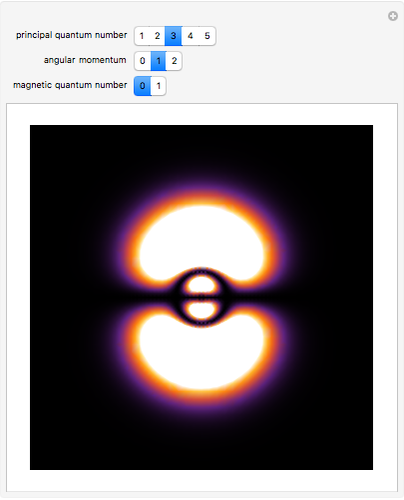
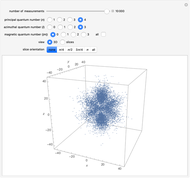
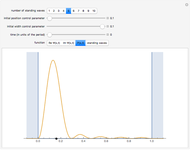
The main goal of this Demonstration is to plot 3D density clouds of the position of the electron in the hydrogen atom in states defined by the three quantum numbers  (principal),
(principal), 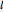 (azimuthal), and
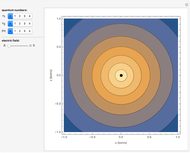
(azimuthal), and 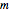 (magnetic). Each dot of the cloud represents a possible result of a measurement of the position of the electron in an individual atom. By imagining that the measurement is repeated many times in different atoms at the same quantum state, you can get a plot representing the probability density function associated with that state. A 2D view can also be obtained by a plane slice containing the
(magnetic). Each dot of the cloud represents a possible result of a measurement of the position of the electron in an individual atom. By imagining that the measurement is repeated many times in different atoms at the same quantum state, you can get a plot representing the probability density function associated with that state. A 2D view can also be obtained by a plane slice containing the  axis. You can select the number of position measurements to be simulated, the quantum numbers
axis. You can select the number of position measurements to be simulated, the quantum numbers  ,
, 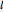 , and
, and 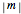 (or all values of
(or all values of 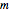 combined in a single plot), and the type of view (3D or 2D). In the 2D slice view you can choose the slice orientation (four possibilities) or all four slices combined for better statistics. The length unit is set equal to the Bohr radius.
combined in a single plot), and the type of view (3D or 2D). In the 2D slice view you can choose the slice orientation (four possibilities) or all four slices combined for better statistics. The length unit is set equal to the Bohr radius.
Contributed by: Carlos Rodríguez Fernández and Andrés Santos (April 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
In spherical coordinates, the wavefunction associated with the quantum state ( ,
, 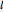 ,
, 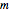 ) is
) is 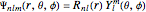 , where
, where  is a spherical harmonic and
is a spherical harmonic and 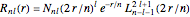 , where
, where 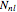 is a normalization constant and
is a normalization constant and 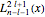 is a generalized Laguerre polynomial. The probability density function,
is a generalized Laguerre polynomial. The probability density function, , is independent of
, is independent of  and of the sign of
and of the sign of 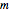 .
.
Reference
[1] R. Eisberg and R. Resnick, Quantum Physics of Atoms, Molecules, Solids, Nuclei, and Particles, New York: Wiley, 1985.
Permanent Citation