Inversive Geometry IV: Inverting a Point with a Compass in Three Steps

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
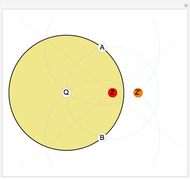
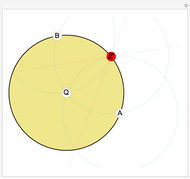
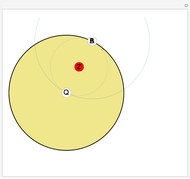
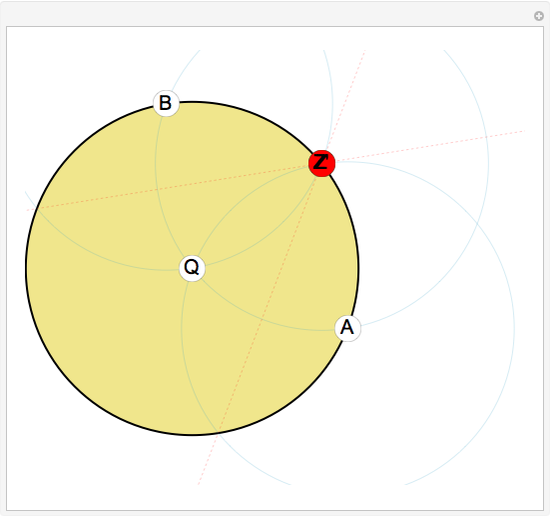
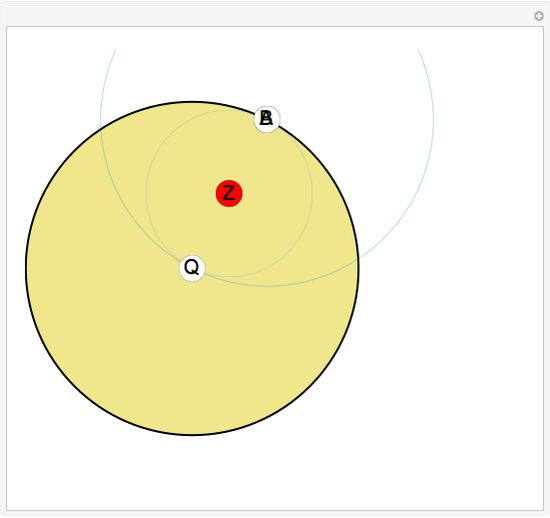
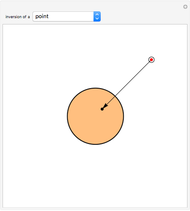
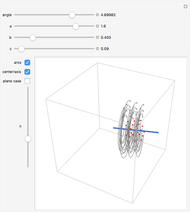
Given a point Z and an inversion circle  with center at point Q and radius
with center at point Q and radius  , consider the following construction to obtain the inverse Z' of Z in
, consider the following construction to obtain the inverse Z' of Z in 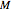 . Draw the circle centered at Z passing through Q; let it intersect
. Draw the circle centered at Z passing through Q; let it intersect 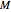 at points A and B. Draw two circles
at points A and B. Draw two circles  and
and  centered at A and B both passing through Q. Their second point of intersection is the inverse of Z in
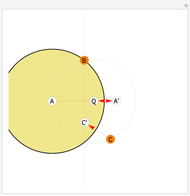
centered at A and B both passing through Q. Their second point of intersection is the inverse of Z in 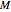 . We justify this by the following reasoning: if we invert
. We justify this by the following reasoning: if we invert 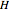 and
and 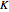 in
in  we obtain (red dotted) lines passing through Z; these lines intersect at
we obtain (red dotted) lines passing through Z; these lines intersect at  and Z, hence their inverses must intersect at the inverses of
and Z, hence their inverses must intersect at the inverses of 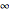 and Z, namely Q and Z'. This Demonstration lets you drag the point Z (red); the construction works for all points Z at a distance from Q greater than
and Z, namely Q and Z'. This Demonstration lets you drag the point Z (red); the construction works for all points Z at a distance from Q greater than  .
.
Contributed by: Jaime Rangel-Mondragon (March 2011)
Open content licensed under CC BY-NC-SA