Inversive Geometry V: Circle through Three Points

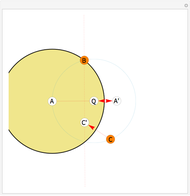
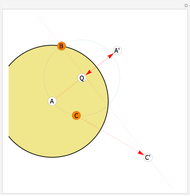
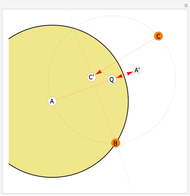
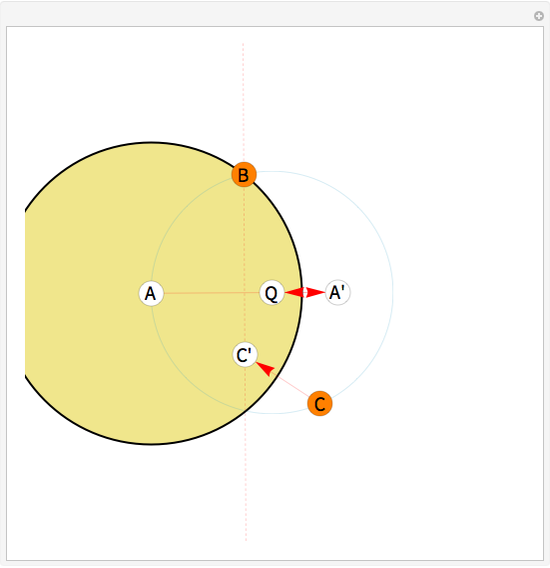
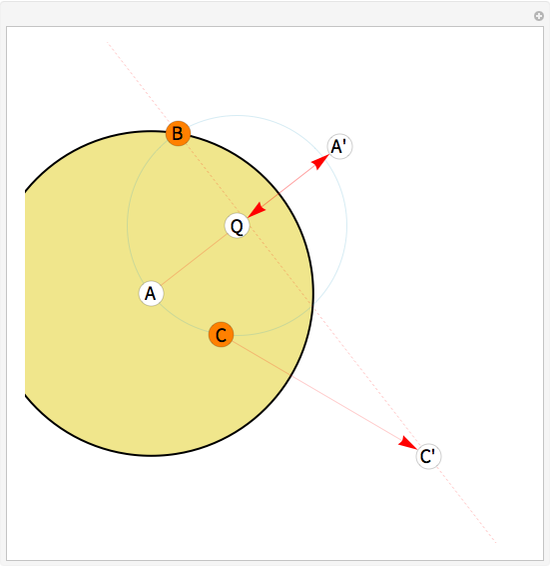
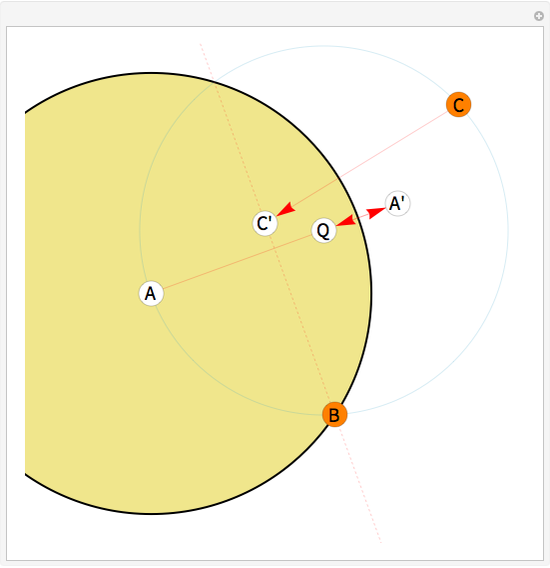
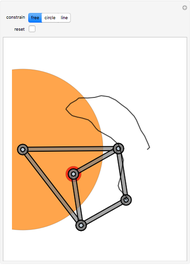
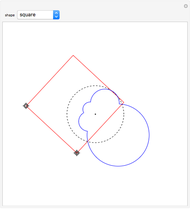
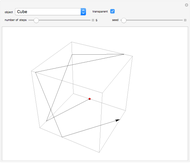
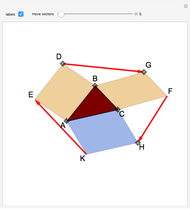
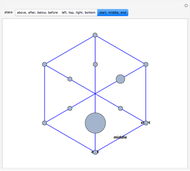
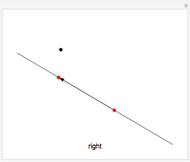
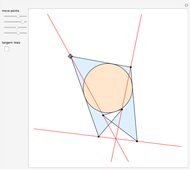
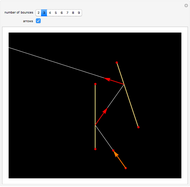
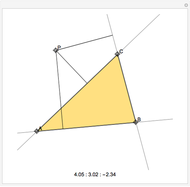
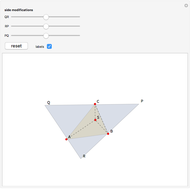
This Demonstration shows how to use a sequence of three inversions to construct a circle passing through three different given points A, B, and C. Let us call its center Q. Let the fixed circle of inversion have center at A and pass through B (orange) and let C' be the inverse of C. Reflect A in the line BC' to get the point A'. Then Q is the result of inverting A'. You can drag the points B or C. Note that this construction still applies if the given points are collinear.