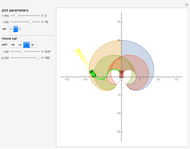
Isochrons for a Dubins Car

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
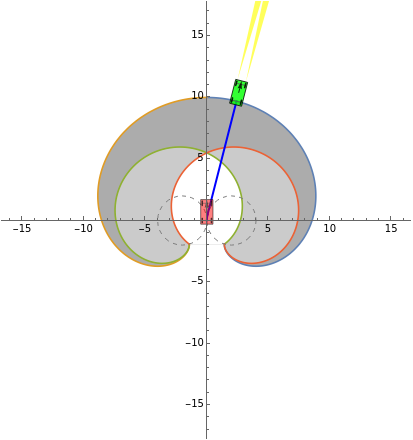
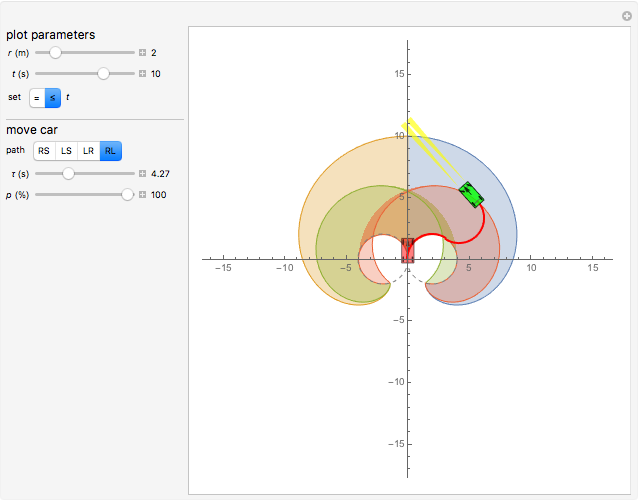
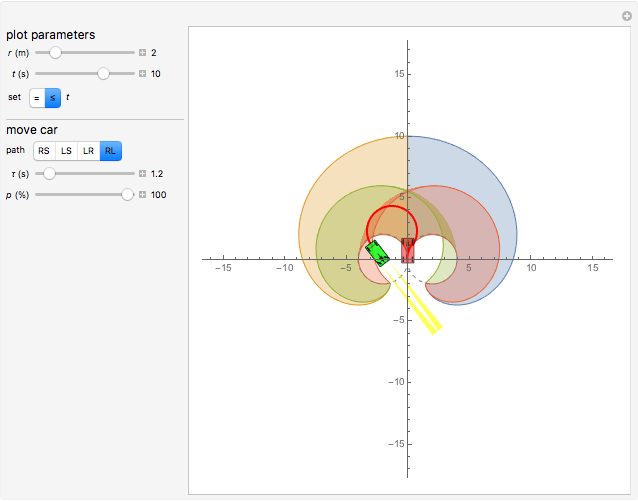
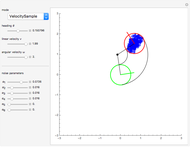
This Demonstration shows the set of  ,
,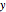 positions reachable at time
positions reachable at time  by a car with a minimum turning radius
by a car with a minimum turning radius  . This set is bounded by four isochrons. An isochron is a line on a diagram or map connecting points relating to the same or equal times. You can choose whether to show areas reachable at time
. This set is bounded by four isochrons. An isochron is a line on a diagram or map connecting points relating to the same or equal times. You can choose whether to show areas reachable at time  or less than or equal to
or less than or equal to  . The boundary of this set is defined by turning at the maximum rate in either direction for
. The boundary of this set is defined by turning at the maximum rate in either direction for  seconds and then either switching directions or moving straight ahead. The percent of the path traveled is denoted by
seconds and then either switching directions or moving straight ahead. The percent of the path traveled is denoted by 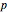 .
.
Contributed by: Aaron T. Becker and Shiva Shahrokhi (December 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
In 1957, Lester Eli Dubins proved that the shortest path between two 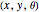 coordinates for a forward-moving vehicle with a minimum turning radius
coordinates for a forward-moving vehicle with a minimum turning radius  is composed entirely of straight lines or no more than three circular arcs of radius
is composed entirely of straight lines or no more than three circular arcs of radius  [1].
[1].
This Demonstration gives the reachable set of  ,
,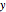 locations from a given starting
locations from a given starting 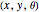 coordinate. The boundary of this set is reachable by a circular arc of radius
coordinate. The boundary of this set is reachable by a circular arc of radius  followed by either a straight path or a circular arc of radius
followed by either a straight path or a circular arc of radius  in the opposite direction. Label a turn to the right at the maximum rate by the letter
in the opposite direction. Label a turn to the right at the maximum rate by the letter 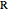 , left as
, left as  and straight as
and straight as 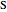 ; then the optimal paths to the boundary are
; then the optimal paths to the boundary are 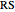 ,
, 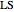 ,
, 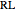 ,
, 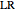 .
.
The Dubins car is a simplified mathematical model of a car that moves on the  ,
,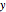 plane [1]. The car's location is specified by the
plane [1]. The car's location is specified by the 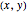 location of the center of the car's rear axle and the orientation
location of the center of the car's rear axle and the orientation  of the car. The car cannot move sideways because the rear wheels would have to slide rather than roll. The Dubins car model stipulates that the car be moving forward at a constant speed and have a maximum steering angle that translates into a minimum turning radius
of the car. The car cannot move sideways because the rear wheels would have to slide rather than roll. The Dubins car model stipulates that the car be moving forward at a constant speed and have a maximum steering angle that translates into a minimum turning radius  . The minimum turning radius circles are drawn tangent to the starting and ending positions with gray dashed circles.
. The minimum turning radius circles are drawn tangent to the starting and ending positions with gray dashed circles.
If the car has forward velocity of 1 unit per second, the system equations are
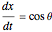 ,
,
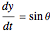 ,
,
and
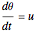 ,
,
where  is chosen from the interval
is chosen from the interval 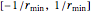 .
.
For a car starting at 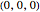 , define the switching time as
, define the switching time as  and arc lengths traveled by the car as
and arc lengths traveled by the car as 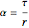 and
and 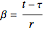 .
.
The car position for an 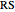 path is
path is
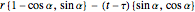 .
.
For 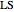 the ending position is
the ending position is
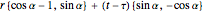 .
.
For 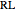 the ending position is
the ending position is
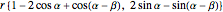 ,
,
and for 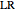 the ending position is
the ending position is
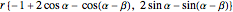 .
.
See [2] for more details.
References
[1] L. E. Dubins, "On Curves of Minimal Length with a Constraint on Average Curvature, and with Prescribed Initial and Terminal Positions and Tangents," American Journal of Mathematics, 79(3), 1957 pp. 497–516. doi:10.2307/2372560.
[2] E. J. Cockayne and G. W. C. Hall, "Plane Motion of a Particle Subject to Curvature Constraints," SIAM Journal on Control, 13(1), 1975 pp. 197–220. doi:10.1137/0313012.
Permanent Citation