Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Isolated Singularities

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

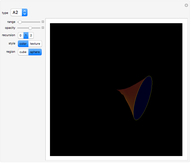
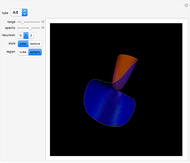
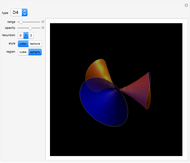
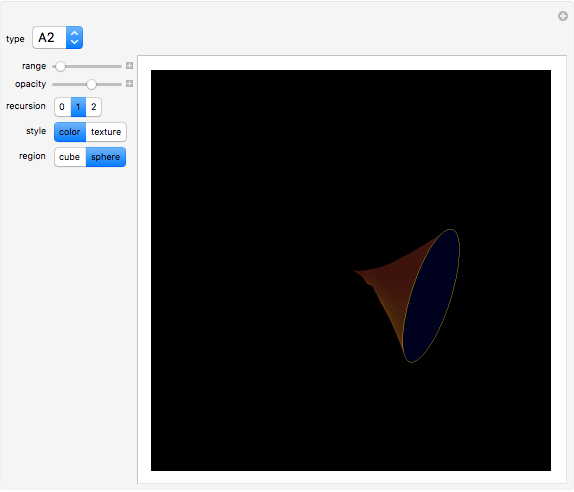
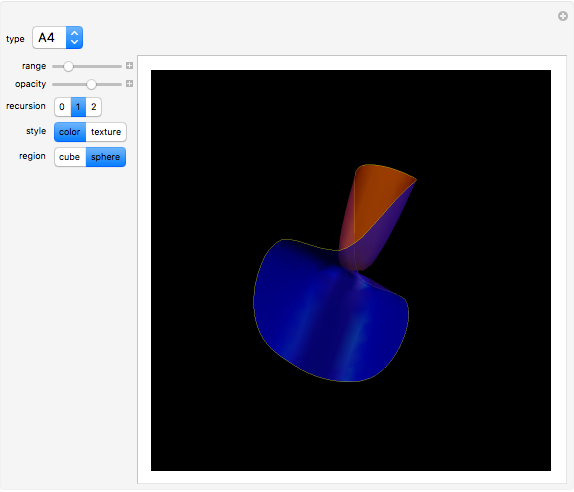
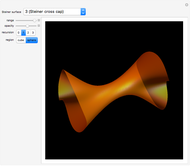
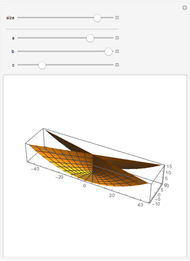
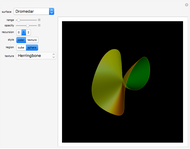
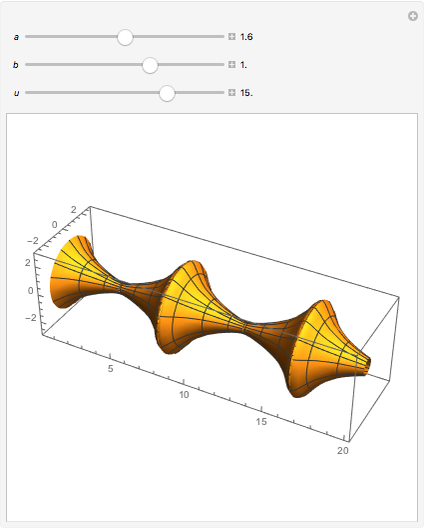
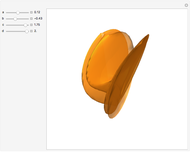
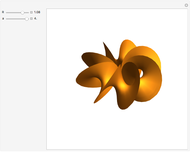
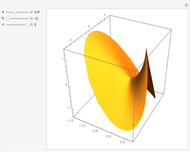
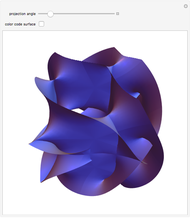
An isolated singularity of a function 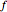is a singularity at a point at which the surface is not differentiable and with no other singularity in a sufficiently small enough neighborhood of . Different types of singularities have been studied and classified; see [1].

Contributed by: Enrique Zeleny (October 2013)
Open content licensed under CC BY-NC-SA

Snapshots

Details

References

[1] GALAAD Project Team. "Classification of Isolated Singularities." (Sept 30, 2013) www-sop.inria.fr/galaad/surface/classification.

[2] S. Holzer and O. Labs, "Illustrating the Classification of Real Cubic Surfaces," Algebraic Geometry and Geometric Modeling, Mathematics and Visualization, Berling: Springer, 2006 pp. 119–134.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send