Optimality of Greedy Change-Making

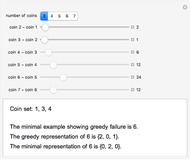
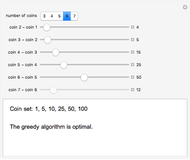
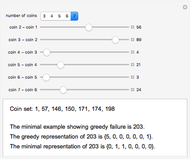
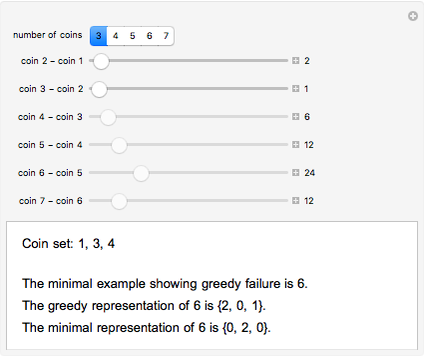
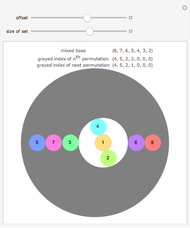
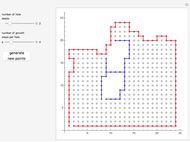
The U.S. coin set of 1, 5, 10, 25, 50, 100 satisfies the greedy condition, meaning that if you make change for an amount 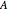greedily (always choosing the largest coin that fits in the amount left) you get a representation of A that uses the fewest possible coins. The old British system based on the halfpenny as the unit corresponds to coins 1, 2, 6, 12, 24, 48, 60, and that system is not greedy: 96 = 48 + 48 but the greedy method gets 96 = 60 + 24 + 12. An efficient algorithm due to Pearson determines whether a set satisfies the greedy condition or not, and if not, finds the smallest target amount that demonstrates the failure. The sliders in the Demonstration control the coin differences, so to see the U.S. system, set to 6 and the differences to 4, 5, 15, 25, 50.