Tiles with Finite Convex Spectra

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
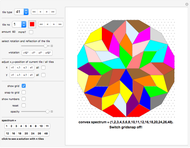
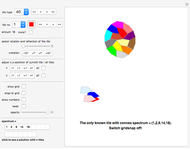
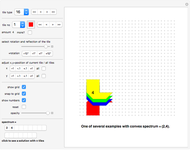
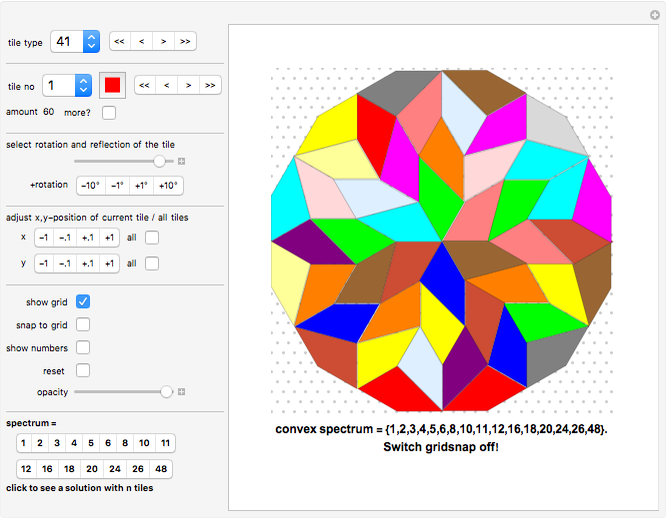
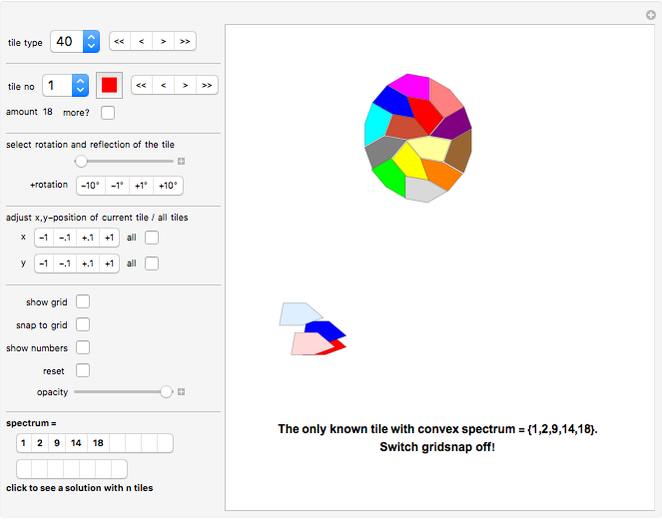
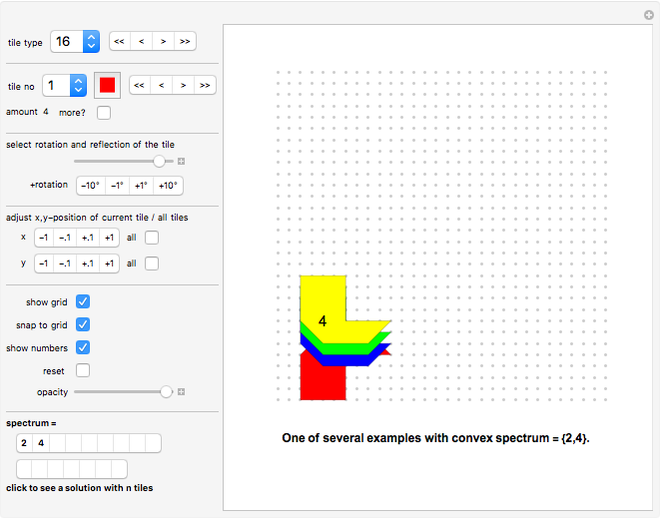
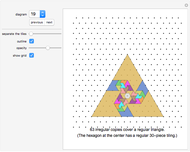
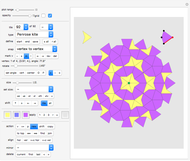
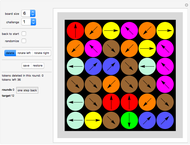
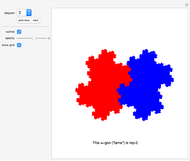
Rearrange the given tiles to create convex shapes.
[more]
Contributed by: Karl Scherer (April 2008)
Additional contributions by: Erich Friedman, Ed Pegg Jr, Mike Reid, Joe DeVincentis andGeorge Sicherman
Open content licensed under CC BY-NC-SA
Snapshots
Details
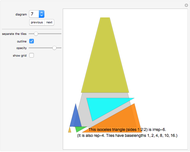
The problem of convex spectra was originally researched by Erich Friedman, Mike Reid, and Karl Scherer in 1999.
The term "convex spectrum" was introduced by Eric Friedman in 1999.
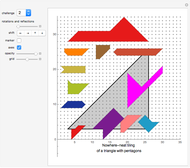
For example, the convex spectrum of a circle is {1}.
The convex spectrum of a half-circle is {1,2}.
This Demonstration considers the mathematical problem of finding all polygons with a finite convex spectrum.
Two interesting examples of tiles with an infinite convex spectrum are also included.
List of convex spectra displayed in this Demonstration:

Controls:
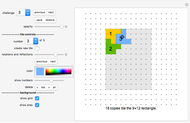
"tile type" pop-up menu Select the tile you want to work with.
"tile no" pop-up menu and color selection Select the tile you want to place. First make sure that you have "show numbers" active (see below).
You can click the color swatch to select a new color for the current tile.
"amount" shows the amount of tiles currently available.
"more?" toggle Click to create one more tile.
"select rotation and reflection of the tile" slider Use the slider select a rotation and reflection of the current tile
The system is designed such that only those rotations are created which relate to the current tile type
(30 degrees increments for tiles on the isometric lattice, 45 degrees on the orthogonal lattice, special rotations for tile types 34 and 39)
"adjust rotation of current tile" SetterBar Click to incrementally change the rotation of the current tile. This adjusting SetterBar is convenient, but necessary only for tile type 39 (all other cases can be solved without using any rotational adjustments).
"adjust x,y-position of current tile" SetterBar
Click to change the coordinates of the current tile.
"all"
Click to adjust all tiles simultaneously.
"show grid"
Click to display orthogonal grid or isometric grid.
"snap to grid"
Click to place the vertices of the current tile on lattice points.
"show numbers"
Click to show the tile numbers.
"reset"
Click to revert to default.
"opacity"
use slider to change transparency.
"spectrum"
Click button titled "n" to see a solution with n tiles
Permanent Citation