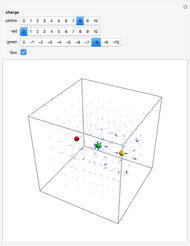
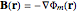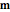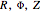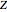Magnetic Field of a Cylindrical Bar Magnet

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
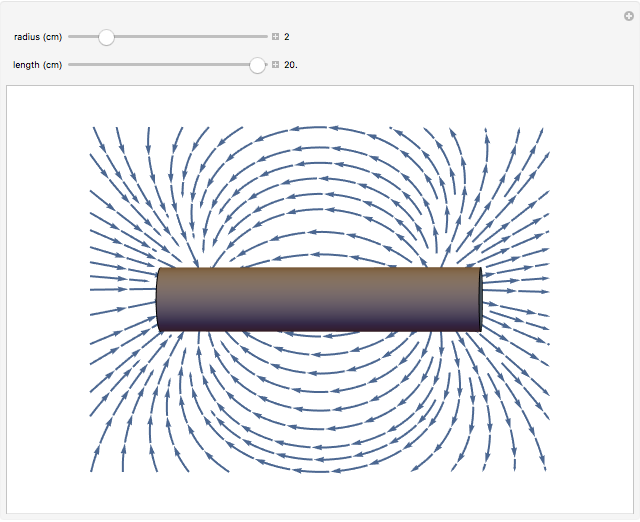
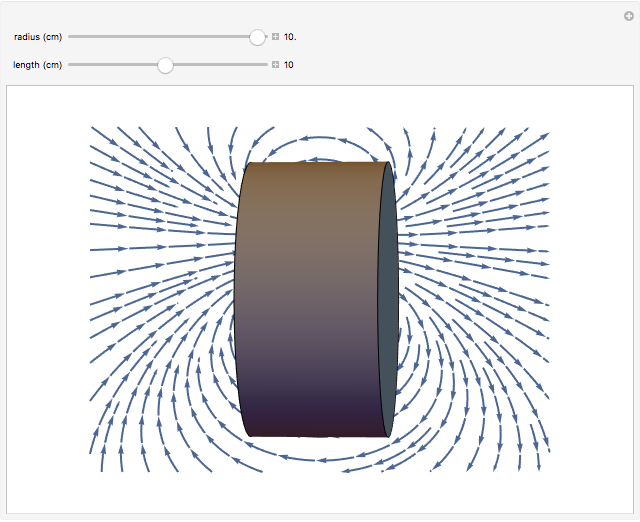
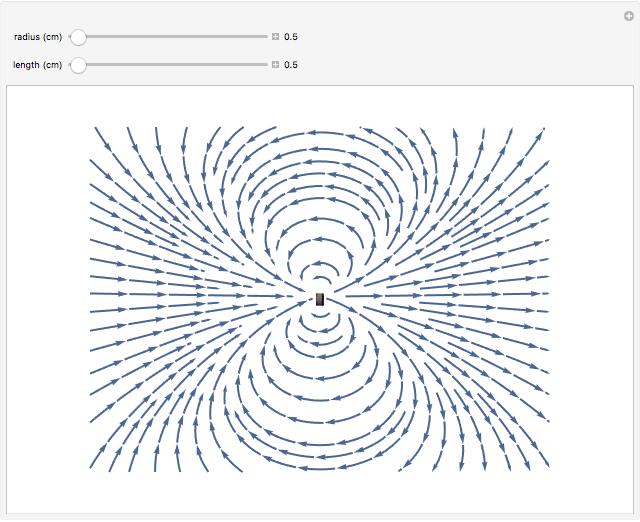
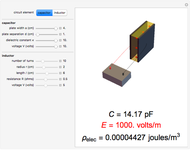
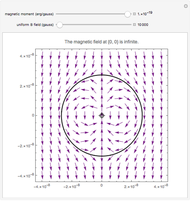
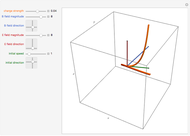
A bar magnet is often approximated simply as a magnetic dipole with north and south magnetic poles separated by a distance 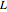 . This is not accurate when the magnet has a significant size, so that magnetic lines of force also emanate from the central portion of the magnet. In this Demonstration, we consider a cylindrical bar magnet of length
. This is not accurate when the magnet has a significant size, so that magnetic lines of force also emanate from the central portion of the magnet. In this Demonstration, we consider a cylindrical bar magnet of length 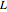 , radius
, radius  , and magnetization
, and magnetization 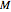 —the magnetic moment per unit volume, which is characteristic of the ferromagnetic material. The magnetization is assumed to be uniform throughout the volume of the magnet, which neglects slight inhomogeneities and possible deviations from the assumed relation
—the magnetic moment per unit volume, which is characteristic of the ferromagnetic material. The magnetization is assumed to be uniform throughout the volume of the magnet, which neglects slight inhomogeneities and possible deviations from the assumed relation 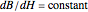 .
.
Contributed by: S. M. Blinder (July 2011)
with suggestions by Evangelos Matsinos
Open content licensed under CC BY-NC-SA
Snapshots
Details
The magnetic scalar potential is given by a triple integral in cylindrical coordinates:
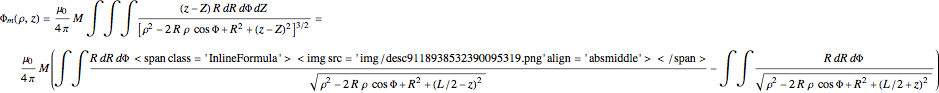
which can be interpreted as originating from two parallel, oppositely charged monopolar disks of radius  separated by a perpendicular distance
separated by a perpendicular distance 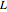 . The result can be expressed in terms of elliptic functions with complicated arguments and the expressions for the magnetic field components
. The result can be expressed in terms of elliptic functions with complicated arguments and the expressions for the magnetic field components 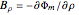 and
and 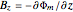 are even more complicated. It is much easier to do the computations numerically, taking advantage of Mathematica's very efficient NIntegrate routines.
are even more complicated. It is much easier to do the computations numerically, taking advantage of Mathematica's very efficient NIntegrate routines.
We thereby obtain:
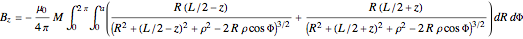
and
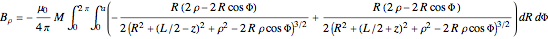 .
.
Permanent Citation